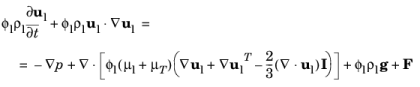
|
•
|
ul is the velocity vector (SI unit: m/s)
|
|
•
|
p is the pressure (SI unit: Pa)
|
|
•
|
ρ is the density (SI unit: kg/m3)
|
|
•
|
g is the gravity vector (SI unit: m/s2)
|
|
•
|
F is any additional volume force (SI unit: N/m3)
|
|
•
|
μl is the dynamic viscosity of the liquid (SI unit: Pa·s), and
|
|
•
|
μT is the turbulent viscosity (SI unit: Pa·s)
|