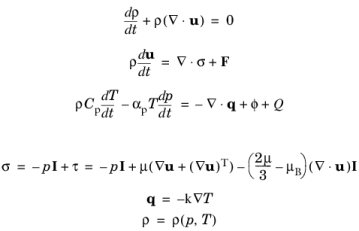In general, the motion of a viscous compressible Newtonian fluid, including the energy equation, is governed by the set of equations listed in Equation 6-4 below.

where the dependent variables are pressure p, velocity u, temperature T, and density ρ. The first three equations are the continuity equation, the momentum equation (the Navier–Stokes equation), and the energy equation, respectively. The last three equation are the constitutive equations. They define the total stress tensor σ and the viscous stress tensor τ through Stokes expression, the Fourier heat conduction law, and an equation of state. See, for example, Ref. 1 to 7 for further details.

The material time derivatives (or total derivatives) d/dt are in the following expanded according to

where A is a dummy variable. The equation of state relates local values of pressure, density, and temperature and is therefore an algebraic equation or an ODE, rather than a PDE. A common form of state equations is to know the density as function of pressure and temperature, ρ = ρ(p, T). In the following, it is assumed that the state equation has this form.

The basic properties of the fluid are the dynamic viscosity μ and thermal conductivity k. The coefficient μB is the bulk (or second) viscosity and describes losses due to compressibility (expansion and contraction of the fluid), where μ describes losses due to shear friction. The bulk viscosity can in some cases be used to model an empirically observed deviation from Stokes’ assumption but is usually negligible compared to μ unless the motion is irrotational; see Ref. 3 and Ref. 4. These three properties are taken to be constant or at most weakly temperature-dependent. The specific heat at constant pressure Cp (per unit mass) and the (isobaric) coefficient of volumetric thermal expansion αp (sometimes denoted α0),

is the viscous dissipation function — that is, the scalar contraction of the viscous stress tensor τ with the rate of strain tensor S. Both tensors are seen as functions of a velocity vector. If the mean velocity is zero, this term vanishes in the following linearization because it is homogeneous of second order in the velocity gradients. Otherwise, it acts as an oscillating source or sink (the term is included in the full Linearized Navier-Stokes interfaces). In the right sides of Equation 6-4, F and Q are a volume force and a heat source, respectively.