For well-defined wave types in infinite domains, an impedance condition exists in every point whereby the pressure and normal velocity are related. Thus, these impedances can be imposed on a boundary to model an infinite, open domain in cases where the wave source inside the domain is either a direction (plane wave), a point (spherical wave) or a line (cylindrical wave). However, be aware that only the boundary-normal component of the velocity is used in the impedance boundary condition while the tangential component is ignored; in cases of nonnegligible tangential components it is recommended to instead use the options Plane Wave Radiation, Spherical Wave Radiation, and Cylindrical Wave Radiation.

see Ref. 6. This is given solely by material parameters and has no user input.

This impedance corresponds to the wave from a point source. It is calculated from the expression (given in Ref. 6)

where x0 is the user-specified location of the point source generating the spherical waves, x is the position of the boundary, and rb is the distance between the two.

This classic infinite-domain wave impedance from an acoustic line source with the user-specified direction and position x0 is presented in, for example, Ref. 6. The expression for the impedance is

where 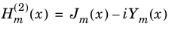is the Hankel function of the second kind of order m given in terms of the Bessel functions of order m of the first and second kind, Jm(x) and Ym(x), respectively. Notice that the source axis vector esa is automatically normalized in this implementation.