The Ray Acoustics Interface

The interface (

), found under the subbranch (

) when adding a physics interface, is used to compute the trajectories, phase, and intensity of acoustic rays. Ray acoustics is valid in the high-frequency limit where the acoustic wavelength is much smaller than the characteristic geometric features. The interface can be used to model room acoustics in concert halls, theaters, class rooms, or car cabins, but also for underwater acoustics, atmospheric acoustics, and other outdoor environments.

The properties of the media in which the rays propagate can be constant within domains, change continuously within domains (graded media) or discontinuously at boundaries. At exterior boundaries it is possible to assign a variety of wall conditions, including combinations of specular and diffuse reflection. Impedance and absorption can depend on the frequency, intensity, and direction of incident rays. Transmission and reflection are also modeled at material discontinuities. A background velocity may also be assigned to any medium to, for example, model the effects of wind in atmospheric acoustics.

•

For a best practice tutorial on room acoustics and impulse response computation, see the Small Concert Hall Acoustics. The Application Library path:

•

For a model of an actual chamber music hall model located in Berlin with comparison to measurements, see the Chamber Music Hall. The Application Library path:

•

For an underwater acoustics tutorial, see the Underwater Ray Tracing Tutorial in a 2D Axisymmetric Geometry tutorial in the COMSOL Application Gallery: https://www.comsol.com/model/44711

For room acoustics applications the impulse response can be determined in postprocessing by combining the information of the simulated rays collected by a dataset and postprocess using the dedicated plot. The energy and level decay curves as well as room acoustic metrics can be computed with the subfeature. For details see the Impulse Response Plot and Receiver Dataset section in Modeling with the Ray Acoustics Interface.

When this physics interface is added, these default nodes are also added to the : , , , and . Then, from the toolbar, add other nodes that implement, for example, boundary conditions. You can also right-click to select physics features from the context menu.

Settings

The is the default physics interface name.

The is used primarily as a scope prefix for variables defined by the physics interface. Refer to such physics interface variables in expressions using the pattern <name>.<variable_name>. In order to distinguish between variables belonging to different physics interfaces, the name string must be unique. Only letters, numbers, and underscores (_) are permitted in the field. The first character must be a letter.

The default (for the first physics interface in the model) is rac.

Ray Release and Propagation

By default, the check box is cleared. Select this check box to model propagation of rays of different frequencies simultaneously. The ray frequency can be specified at release features by entering a value or expression, sampling the frequency from a distribution, or entering a list of values. If this check box is cleared, the frequency is the same for all rays and is specified in the settings for the Ray Properties node.

Regardless of whether the check box is selected, properties at walls can depend on the frequency (variable rac.f) of each ray released. Domain material properties, like the speed of sound, can also depend on the frequency. Entering a frequency distribution of the released rays also enables emitting more complex source signals (decomposed in their Fourier components).


	To define the speed of sound or another medium property as a function of ray properties such as the ray frequency or intensity, the ray variable must be enclosed in the noenv() operator. For example, to use the ray frequency rac.f in an expression for the speed of sound, it must be included as part of the expression noenv(rac.f). See also Medium Properties.

The prevents an inordinate number of rays from being generated by capping them at the number supplied in the text field. The default is 500. Rather than being produced directly by release features such as the Release from Grid node, secondary rays are released when an existing ray is subjected to certain boundary conditions. For example, when a ray undergoes refraction at a Material Discontinuity between different media, the incident ray is refracted and a reflected ray is created; the degrees of freedom for this reflected ray are taken from one of the available secondary rays, which are preallocated when the study begins.

If an insufficient number of secondary rays are preallocated, a reflected ray may not be released when an existing ray undergoes refraction. Thus, the should be large enough that all reflected rays which significantly affect the solution can be released.

Material Properties of Exterior and Unmeshed Domains

Enter a value or expression for the cext (SI unit: m/s). The default value is 343[m/s]. Then enter a value or expression for the ρext (SI unit: kg/m3). The default value is 1.2[kg/m^3].

When one of the options is selected (see below), select an option from the list:

•

For (the default), enter a value or expression for the αext (SI unit: Np/m). The default is 0.

•

For , enter a value or expression for the mext (SI unit: Np/m). The default is 0.

•

For , enter a value or expression for the α’ext (SI unit: dB/m). The default is 0.

•

For , enter a value or expression for the

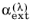(SI unit: dB). The default is 0.

A more detailed explanation of each definition of the attenuation coefficient is given in the Medium Properties section.

These material properties are used when tracing rays outside the geometry or when tracing rays through domains that are not included in the selection of the Ray Acoustics physics interface. That is, meshless ray tracing. The medium properties in the deselected and exterior void domains must be constant and cannot be functions of any field variables, such as temperature. The properties like the attenuation can depend on a parameter like the band center frequency when modeling room acoustics applications, see the Impulse Response Plot and Receiver Dataset section.

Intensity Computation

Select an option from the list: (the default), , , , , or . For the ray intensity and power is not computed.

•

For , auxiliary dependent variables are used to compute the intensity of each ray. For a complete list of the auxiliary dependent variables that are defined, see Intensity and Wavefront Curvature in Theory for the Ray Acoustics Interface. This option is more accurate and is usually less computationally demanding than , but is only valid for computing intensity in homogeneous (constant speed of sound) media.

•

For , the total power transmitted by each ray is defined as an auxiliary dependent variable, in addition to the auxiliary dependent variables that are declared when is selected. Like intensity, the power is affected by absorbing media and by reflection or refraction at boundaries. Unlike intensity, ray power does not change due to the convergence or divergence of a bundle of rays. The Sound Pressure Level Calculation subnode is available for the Wall feature. The option is necessary for the impulse response postprocessing, see Impulse Response Plot and Receiver Dataset.

•

The option combines the dependent variables created by the and options.

•

For , auxiliary dependent variables are used to compute the intensity of each ray. The intensity is affected by gradients in the speed of sound. Graded media may be present, for example, when modeling the effect of the saline climb in underwater acoustics. For a complete list of the auxiliary dependent variables that are defined, see Intensity and Wavefront Curvature in Theory for the Ray Acoustics Interface. This intensity computation method is valid for both homogeneous and graded media. If all media are homogeneous, meaning that the gradient of the speed of sound is zero everywhere except at material discontinuities, then it is recommended to select instead, since it is the more accurate intensity computation method for such cases.

•

For , the total power transmitted by each ray is defined as an auxiliary dependent variable, in addition to the auxiliary dependent variables that are declared when is selected. The Sound Pressure Level Calculation subnode is available for the Wall feature. If all media are homogeneous then it is recommended to select instead.

When the ray intensity or power is solved for (one of the options , , , , or is selected), a list for the appears. Select (the default) to set the reference pressure to 20 μPa, to set the reference pressure to 1 μPa, or to enter a value or expression in the text field. The reference pressure is used to calculate the sound pressure level (variable rac.Lp) and sound intensity level (variable rac.LI) along rays.

If the ray intensity is solved for (one of the options , , , or is selected), the check box is available. By default, the check box is cleared. Select this check box to compute the phase along each ray. An auxiliary dependent variable for the phase rac.Psi is created. The phase changes along the ray trajectory based on its frequency and is also subjected to phase shifts that happen at walls with specular reflection and absorption.

When or is selected from the list, enter a (dimensionless). This tolerance is used internally when computing the principal radii of curvature in a graded medium, and is used to define a criterion by which both principal radii of curvature are declared approximately equal. A larger tolerance makes the solution less accurate but more stable.

Additional Variables

Select the check box to allocate an auxiliary dependent variable for the number of reflections undergone by each ray, including reflections by the Wall and Material Discontinuity features. The auxiliary variable begins at 0 when rays are released and is incremented by 1 every time a ray is reflected at a boundary. The option is necessary for the impulse response postprocessing, see Impulse Response Plot and Receiver Dataset.

By default, the check box is cleared. Select this check box to add new variables for quantities that cannot necessarily be recovered from the ray trajectory data alone. This is especially true if automatic remeshing has been used in a model. The following variables are created:

•

The release time of a given ray (variable name rac.rti).

•

The time at which a ray stopped at a boundary (variable name rac.st).

•

The final status of the ray (variable name rac.fs). This indicates the status of a ray at the final time step. The value is an integer which has one of the following values:

0 for unreleased rays

1 for rays that are still in the modeling domain

2 for frozen rays

3 for stuck rays

4 for rays that have disappeared.

To summarize the total number of rays having each final status, the following global variables are also defined.

Table 8-1: Global Variables Based on Ray Status
Name	Description
fac	Fraction of active rays at final time step
fds	Fraction of disappeared rays at final time step
ffr	Fraction of frozen rays at final time step
fse	Fraction of secondary rays released
fst	Fraction of stuck rays at final time step
nsr	Number of released secondary rays
nsrf	Number of released secondary rays at final time step
nsu	Number of unreleased secondary rays
nsuf	Number of unreleased secondary rays at final time step

The global variable names in Table 8-1 all take the unreleased secondary rays into account. For example, suppose an instance of the Ray Acoustics interface includes 100 primary rays and 100 allocated secondary rays. At the last time step, suppose that 80 of the primary rays have disappeared at boundaries and that 40 secondary rays have been emitted, all of which are still active. Then the variable rac.fac, the fraction of active rays at the final time step, would have the value (20 + 40)/(100 + 100) or 0.3.

Advanced Settings

This section is only shown when are enabled (click the button in the toolbar).

The sets the accuracy order of the time stepping used for time steps during which a ray-wall interaction happens. Select an order of to use a forward Euler step and compute the motion both before and after the wall collision. Select an order of (the default) to use a second-order Taylor method and compute the motion before the wall collision. After the collision a second-order Runge-Kutta method is used.

Select an option from the list: , , or . This setting determines how the additional argument to random functions is defined in features such as the Wall boundary condition with the wall condition. Typically, the random numbers are functions of the ray index, position, time, and another argument i, which is defined as follows:

•

For , the additional argument is based on the position of each node in the Model Builder. As a result, random numbers generated in different nodes are created independently of each other, but the same result can be reproduced by running the same study several times.

•

For , the additional argument is randomly created, causing the random functions to return different results each time the study is run.

•

For , the additional argument is defined by a user input in the window each feature. Independent solutions can be obtained by running a parametric sweep for different values of i.

The check box, which is cleared by default, allows an array of release times for the rays to be specified in any of the ray release features. If the check box is cleared, all rays are released at time t = 0.

By default the check box is cleared. If this check box is selected, then expressions for the time derivatives of the degrees of freedom on rays are not included in the Jacobian matrix. Excluding contributions to the Jacobian can significantly improve solution time. The drawback is that the Jacobian is not exact, so smaller time steps or path length intervals may be needed to obtain an accurate solution. This drawback is most noticeable when computing the ray intensity or power in attenuating media.

By default, the check box is selected. Certain ray release features, such as the and features, compute the ray release positions based on a geometric entity, which must be meshed. While this check box is selected, failure to mesh the selections of such features will result in an error message when running any study in the model. If this check box is cleared, failure to mesh the selections of such features will result in them releasing zero rays, but will otherwise not interrupt the computation. Other physics features will still be able to release rays normally.

Enter a value for the . The default value is 1000. If a ray undergoes more than the specified number of boundary interactions in a single time step taken by the solver, the ray will disappear. This is included as a safeguard to prevent rays from getting stuck in infinite loops if the time between successive ray-wall interactions becomes infinitesimally small.

Dependent Variables

The dependent variables (field variables) are the and . The name can be changed but the names of fields and dependent variables must be unique within a model.


	Theory for the Ray Acoustics Interface