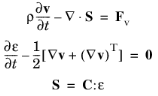You are viewing the documentation for an older COMSOL version. The latest version is
available here.
The Elastic Waves, Time Explicit Model node adds the equations for modeling the propagation of linear elastic waves. Define the properties of a general isotropic or anisotropic material. The model solves the governing equations for a general linear elastic material in a velocity-strain formulation
where v is the velocity,
ρ the density,
S the stress tensor,
ε the strain tensor,
C is the elasticity tensor (or stiffness tensor), and
Fv is a possible body force. The equations are valid for both isotropic and anisotropic material data. Bulk dissipation can be added by using the
Damping subnode.
The Global coordinate system is selected by default. The
Coordinate system list contains all applicable coordinate systems in the component. The coordinate system is used for interpreting directions of orthotropic and anisotropic material data and when stresses or strains are presented in a local system.
Define the Solid model representation of the material. Choose:
|
•
|
Isotropic for a linear elastic material that has the same properties in all directions.
|
|
•
|
Orthotropic for a linear elastic material that has different material properties in orthogonal directions, so that its stiffness depends on the properties Ei, νij, and Gij.
|
|
•
|
Anisotropic for a linear elastic material that has different material properties in different directions, and the stiffness comes from the symmetric elasticity matrix, D
|
If orthotropic or anisotropic is selected then also select the Material data ordering to
Voigt (the default) or
Standard notation. This option defines what numbering and notation is used for entering user defined material data and when defining material properties in the
Materials node.
For an Isotropic Solid model, from the
Specify list select a pair of elastic properties for an isotropic material —
Young’s modulus and Poisson’s ratio,
Young’s modulus and shear modulus,
Bulk modulus and shear modulus,
Lamé parameters, or
Pressure-wave and shear-wave speeds. For each pair of properties, select from the applicable list to use the value
From material or enter a
User defined value or expression.
|
•
|
Shear-wave speed (transverse wave speed) cs. This is the wave speed for a solid continuum.
|
When Orthotropic is selected from the
Solid model list, the material properties vary in orthogonal directions only. The
Material data ordering can be specified in either
Standard or
Voigt notation. When
User defined is selected in 3D, enter three values in the fields for
Young’s modulus E,
Poisson’s ratio ν, and the
Shear modulus G. This defines the relationship between engineering shear strain and shear stress. It is applicable only to an
orthotropic material and follows the equation
|
|
νij is defined differently depending on the application field. It is easy to transform among definitions, but check which one the material uses.
|
When Anisotropic is selected from the
Solid model list, the material properties vary in all directions, and the stiffness comes from the symmetric
Elasticity matrix,
D. The
Material data ordering can be specified in either
Standard or
Voigt notation. When
User defined is selected, a 6-by-6 symmetric matrix is displayed.
|
|
Note that the 6-by-6 Elasticity matrix, D has to be complete regardless of the spatial dimension of the problem. This is due to the generalized plane strain formulation of the governing equations solved in 2D.
|
The default Density ρ uses values
From material. For
User defined enter another value or expression. If any material in the model has a temperature dependent mass density, and
From material is selected, the
Volume reference temperature list will appear in the
Model Input section. As a default, the value of
Tref is obtained from a
Common model input. You can also select
User defined to enter a value or expression for the reference temperature locally.
To display this section, click the Show More Options button (

) and select
Stabilization in the
Show More Options dialog box. In this section, you specify the value of the
Lax–Friedrichs flux parameter τLF (default value: 0.2). This value controls the numerical flux between the elements (nodal discontinuous Lagrange elements) used with the discontinuous Galerkin (dG) method. The numerical flux defines how adjacent elements are connected and how continuous
v and
E are. Different definitions of the numerical flux lead to different variants of the dG method. The flux implemented here is the so-called global Lax–Friedrichs numerical flux. The value of the parameter
τLF should be between 0 and 0.5. For
τLF = 0 a so-called central flux is obtained. Setting
τLF = 0.5 gives a maximally dissipative global Lax–Friedrichs flux.
To display this section, click the Show More Options button (

) and select
Advanced Physics Options in the
Show More Options dialog box. By default, the filter parameters
α,
ηc, and
s are not active. Select the
Activate check box to activate the filter. The filter provides higher-order smoothing for the dG formulation and can be used to stabilize the solution. Inside absorbing layers the settings given here are overridden by the
Filter Parameters for Absorbing Layers.
Enter values for the filter parameters in the corresponding text fields (default values: 36, 0.6, and 3). α must be positive and lie between 0 and 36.
α = 0 means no dissipation and
α = 36 means maximal dissipation.
ηc should be between 0 and 1, where 0 means maximal filtering and 1 means no filtering (even if filtering is active). The
s parameter should be larger than 0 and controls the order of the filtering (a dissipation operator of order 2
s). For
s = 1, you get a filter that is related to the classical 2nd-order Laplacian. A larger s gives a more pronounced low-pass filter.
To display this section, click the Show More Options button (

) and select
Advanced Physics Options in the
Show More Options dialog box. The maximum wave speed enters the expression for the
cell wave time scale used by the solver to estimate a stable internal time step. Select
Automatic (the default) or
User defined. With the
Automatic option the maximum speed is set equal to the pressure wave speed, for
User defined enter another value for
cmax. The estimate for isotropic materials is correct, but for certain configurations of anisotropic materials it can be necessary to enter a larger value to ensue numerical stability.