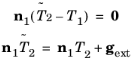Forces on an Elastic Solid Surrounded by Vacuum or Air
Consider a solid (Material 1) surrounded by vacuum (Material 2). It is natural to associate the surface force on the boundary between the materials with the solid. In many applications air can be approximated by vacuum.
In practice, the equation for the force balance also needs to include an external boundary force gext. It is nonzero on those parts of the boundary where it is necessary to compensate for the contributions to the stress tensor that you are not interested in or do not have enough information on. These contributions come from the influence of the adjacent domains. By approximating the surroundings by vacuum or air, the influence of these boundaries and their adjacent domains (that are not part of our model) on the electromagnetic fields are neglected.
On the boundary, the following equations apply:
The external boundary force gext can represent the reaction force from another body that the solid is attached to.
The equations for the balance of forces on the solid now become
For calculating the total force F on the solid these equations need to be integrated over the entire solid and the solid/vacuum boundary
According to the divergence theorem:
this means that the external force
is needed to balance the term for the boundary integral of the stress tensor in the surrounding vacuum
to keep the solid stationary. That is Fext + F = 0. If the external forces are suddenly removed, the solid is no longer stationary, but F causes the solid to begin to move with an initial acceleration according to
where m is the total mass and a is the acceleration of the solid.
To summarize, the total force, F, is computed as a boundary integral of the stress tensor in vacuum on the outside of the solid. To obtain this result, the contribution from the air pressure gradient has been neglected. This is equivalent of assuming that ∇ · T2 = 0. A more detailed treatment shows that the pressure gradient contributes with a lifting (buoyancy) force on the solid.