The Embedded Reinforcement multiphysics coupling provides a generic method to couple lower dimension structural elements to a solid domain. Mesh elements from the Truss, Beam, or Membrane interfaces within or adjacent to a solid domain can be connected by adding this multiphysics coupling. Two different formulations are available for connecting the interfaces: Rigid or Spring connection. The rigid connection is based on a pointwise constraint formulation, while the spring connection is based on a penalty regularization of the constraint. When using the spring connection, a nonlinear behavior can be included by adding a bond slip model.

To facilitate the connection between the solid domain and the embedded structure, a nonlocal coupling is set up between the two interfaces. This coupling is made through a General Extrusion operator that maps an expression defined on the source to an expression that can be evaluated on the destination geometry. Here, the source is always the solid domain, and the destination is the embedded thin structure. The latter can be either a Truss, Beam, or Membrane interface. Mathematically, the mapping of a generic expression E from a source domain Ωsrc to a point Xdst on the destination boundary (or edge) Γdst can be described by

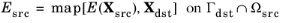
The mapping is such that for each point Xdst, it finds the closet point Xsrc in Ωsrc at which to evaluate E. From Equation 3-165 it is inferred that the mapping is made in the material frame, that is, the mapping is constant even for a geometrically nonlinear case. Moreover, the mapping is only valid for the part of Γdst that lies within Ωsrc.

With the definition in Equation 3-165, the rigid connection type is described by adding a constraint on Γdst such that the displacement field u equals

The penalty connection is set up by first defining a relative displacement vector Δu between the mapped source and the destination

From the relative displacement vector Δu, the spring force f of the penalty formulation is defined by Hooke’s law

where K is the spring stiffness matrix, which has nonzero components on the diagonal only. The spring stiffness matrix K is most naturally described in the local coordinate system of the thin structure, Γdst, such that the spring force fl in local coordinates is defined by

where T is the transformation matrix form local to global coordinates and Kl is the spring stiffness matrix in the local coordinate system. The local coordinate system is either defined by the destination physics interface, or automatically by the multiphysics coupling. Finally, the following weak contribution is added

When a Bond slip model is added to the spring connection, an additive decomposition of Δu into elastic and plastic counterparts is assumed so that, in the local coordinate system we get

where ul,e is the elastic displacement, and ul,p is the plastic displacement (or slip) on the destination. The definitions of the spring force and the weak contribution are unaffected.

The slip vector ul,p is defined through a local constitutive model based on the flow theory of plasticity. When the destination physics is either a Truss or a Beam interface, slip can only occur in the direction of the local edge tangent, which means that the slip vector is defined by a single scalar value, that is, ul,p = {0,0,upn}. The constitutive model is then summarized by

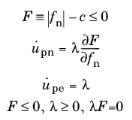
where fn and upn is the spring force and slip in the direction of the local edge tangent, respectively. The cohesion c determines the sliding resistance, and it can depend on any variable or field present in the model. The plasticity model is defined by the yield function F, the plastic multiplier λ, and the accumulated slip upe. The last row of Equation 3-166 are the Kuhn-Tucker conditions.

When the destination physics is a Membrane interface, sliding can only occur in the direction of the local tangents of the plane given by the normal of the boundary, that is, ul,p = {ut1,ut2,0}. The constitutive model then takes a slightly different form, and it can be summarized by

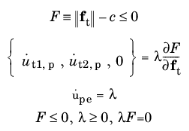
where ft is a vector containing the two tangent components of the local spring force fl.

The rate equations in the constitutive models given by Equation 3-166 and Equation 3-167 are implemented through a backward Euler discretization. The resulting set of nonlinear algebraic equations is solved using Newtons method to find λ, upe, and ul,p. Optionally, it is also possible to compute the dissipated energy due to friction, Wp, by also solving the following rate equation