Periodic Cell Theory
The heterogeneous properties of a material in the microscopic scale are often unfeasible to use directly on a macroscopic scale, in which a structure is typically analyzed. There one needs to use a homogeneous material model, but with appropriately averaged properties.
The Cell Periodicity feature facilitates the evaluation of such average properties. It is based on the idea of a representative volume element (RVE). The RVE is a domain that is representative for the material on a microscopic scale.
An RVE is typically identified as the smallest possible unit cell of a material. If the material has a random distribution of for example porosity, it should be large enough to be representative for the average properties of the material on a macroscopic scale.
The only requirement on the shape of the RVE is that it should be possible to fill space with a repetitive pattern of RVEs. This means that there are a set of matching boundary pairs, each of them having the same geometry, but offset by a given distance.
To model an RVE, you add a Cell Periodicity node, and select the domains representing the unit cell. For each pair of matching boundaries, add a Boundary Pair subnode, and select the boundaries.
In principle, there are no limitations on the physics features you can use for modeling the RVE, as long as the basic assumptions about periodicity are not violated. You should however not add any displacement constraints, since the possible rigid body motions are automatically constrained by the Cell Periodicity node.
Homogenization Method
The homogenization method introduces two scales: a macro scale and a micro scale. The macro scale usually refers to the homogenized continuous media, and the micro scale to the heterogeneous unit cell, that is, the RVE. The macro stress tensor and the macro strain tensor are derived by averaging the stresses and strains in the periodic cell
(3-136) and
where V is the volume of the cell. The macroscopic elasticity tensor of the homogenized continuum is then defined by
(3-137)
Displacement Continuity
For a periodic structure that consists of an array of repeated unit cells, the displacement field is written as
where 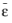is global average strain tensor, and u* is a function that is periodic from one unit cell to another. As the array of cells is a continuous structure, displacement continuity must be satisfied across the boundaries between the cells. The boundaries in a Boundary Pair subnode must always appear in parallel pairs. One of them is labeled as source and the other as destination. The displacements on a pair of parallel and opposite boundary surfaces can be written as
and
Hence, the displacement continuity is established by
(3-138)
Together with displacement continuity, the traction continuity should be satisfied for the RVE, which is done implicitly in the displacement based finite element method. There are different options available to enforce the displacement continuity constraint:
•
Free Expansion
•
Prescribed Average Strain
•
Prescribed Average Stress
•
Mixed
Free Expansion
In order to determine the homogeneous coefficient of thermal expansion of a heterogeneous material, the material is subjected to unit rise in temperature, while it is allowed to expand freely. To model this behavior, the global average strain tensor in Equation 3-138 is considered as a global degree of freedom that varies freely. The averaged coefficient of thermal expansion α is computed as
Similarly, to determine the homogeneous coefficient of hygroscopic swelling, the material is subjected to a unit rise in concentration. The averaged coefficient of hygroscopic swelling β is then computed as
If no averaged properties are computed, the free expansion option only computes the average stress and strain tensors by enforcing Equation 3-138 as a constraint.
Prescribed Average Strain
In order to determine the homogeneous elasticity tensor of a heterogeneous material, the material is subjected to a unit strain in each direction, one-by-one, while keeping the other strain components equal to zero. To model this behavior, the global average strain tensor in Equation 3-138 is a user input. The average stress is computed from Equation 3-136, and the elasticity tensor is obtained from Equation 3-137.
Prescribed Average Stress
In order to determine the homogeneous compliance tensor of a heterogeneous material, the material is subjected to a unit stress in each direction, one-by-one, while keeping the other stress components equal to zero. The average stress is a user input, and the global average strain tensor in Equation 3-138 is a global degree of freedom, which is defined by a global weak equation
(3-139)
The compliance tensor is then obtained from the following equation
Mixed
This option studies the response of the unit cell when subjected to a combination of prescribed stress and strain. You can chose which components of the average stress and strain tensors to enter as user inputs; the remaining components are computed from Equation 3-136 and Equation 3-139 by enforcing Equation 3-138 as a constraint.