Spring-Damper Theory
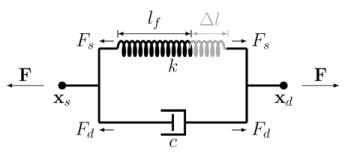
The Spring-Damper node is used to define elastic and dissipative forces between a source and a destination attachment. Two different spring types are available. When using the directional spring (Figure 3-32), all forces act in the direction of the spring extension. With the matrix spring formulation, more general dependencies between the displacements and forces can be defined.
Figure 3-32: Conceptual sketch of a Spring-Damper.
•
Connection Points and Spring Extension
•
Deactivation
•
Spring and Damping Forces
•
Spring and Damping Energies
Connection Points and Spring Extension
The current position of the source and destination points, xs and xd, can be written as
where Xs and Xd are the original positions of the two points, and us and ud are their respective displacements. For the special case where the source point is selected as a fixed point,
The relative displacements between the source and destination points determines the forces in the spring-damper. Depending on the chosen spring type (directional or matrix), the relative displacement is defined by different quantities.
Directional
For the directional spring, the extension is given in terms of a scalar spring length. The initial spring length, l0, is
The current spring length, l, is
In the case of a geometrically linear analysis, the current spring length is linearized to
In addition to the initial geometrical distance between the two points you can specify an initial spring extension Δl0, so that the free length of the spring is
You can also specify the free length of the spring explicitly.
The spring extension Δl is computed as the difference between the current spring length and the free length,
Matrix
When choosing the matrix spring type, the spring-damper forces are instead computed based on the relative displacement and the relative rotation vectors. If the study is geometrically linear, the relative rotation vector is
where Θs and Θd are the rotations of the source and destination attachments, respectively. In case of geometrically nonlinear studies, the relative rotation vector is instead computed from the quaternion multiplication,
where qs and qd are the source and destination rotations represented by unit quaternions, and Δq is a quaternion representing the differential rotation, which can be converted to an axis-angle representation defining the relative rotation vector.
By default, the relative displacement vector is simply defined as
If the check box Include rotational contribution in displacement in the Spring-Damper section is selected, an additional term is included in the relative displacement vector which can be interpreted as the displacement at the tip of a bar element which connects the source and destination due to the rotation at the destination point. In a geometrically linear study, the relative displacement is then defined as
In a geometrically nonlinear study, the cross-product is replaced with the rotation matrix.
Deactivation
The spring-damper can be deactivated under certain conditions. In terms of the implementation, this means that many expressions are multiplied by an activation indicator, iac. The activation indicator has the value 1 when the component is active, and 0 when deactivated.
Spring and Damping Forces
Spring and damper forces are computed differently for the directional and the matrix spring types.
Directional
When the directional spring is chosen, the spring force is proportional to the spring constant k:
If k depends on the extension, so that the spring is nonlinear, it should be interpreted as a secant stiffness, that is
You can also specify the spring force as function of extension explicitly, as
To create the expression for the function, use the built-in variable for the spring extension. It has the form <physicsTag>.<SpringNodeTag>.dl, for example solid.spd1.dl.
In a dynamic analysis, the viscous damping force is computed as
where c is the viscous damping coefficient.
The magnitude of the total force is
The total forces in the global coordinate system, acting on the destination and source points are
In a geometrically linear case, the orientation of the force is kept fixed, so that
The contribution to the virtual work is
Matrix
When choosing the matrix formulation, the spring and the damper forces are computed from the relative displacements and rotations. In the most general case, the spring-damper force, F, and the spring-damper moment, M, are
where the subscripts s and d refer to the spring and damper, respectively; the different k and c represent sub-matrices of size 3x3, describing the elastic and the dissipative forces and moments. In 2D, some of the matrices related to the rotation and to the translational-rotational coupling have components which are zero by definition.
Spring and Damping Energies
In stationary and time-dependent analysis, the elastic energy in the spring is computed.
Directional
With the directional spring formulation, the energy is
In a time-dependent analysis, the energy dissipated in the damper, Wd, is computed using an extra degree of freedom. The following equation is added:
In a frequency domain analysis, the elastic energy in the spring and the energy dissipated in the damper are computed as
These energy quantities represent the cycle average, and only the perturbation terms are included.
Matrix
If instead the matrix formulation is used, the elastic energy in the spring is
In a time-dependent analysis, the energy dissipated in the damper, Wd, is computed using an extra degree of freedom. The following equation is added:
In a frequency domain analysis, the elastic energy in the spring and the energy dissipated in the damper are computed as