The direct electrostrictive effect for a material of arbitrary symmetry can be represented as the following additive contribution to the strain (Ref. 3):

which is quadratic in polarization P in contrast to linear piezoelectricity.

The fourth order tensor Q can be effectively represented by a 6-by-6 coupling matrix. Further simplification due to material symmetry is possible in most cases. For example, for piezoelectric ceramics, the coupling matrix can be characterized by three independent components: Q11, Q12, and Q44.

where ε0,vac is the electric permittivity of free space, and χ is the linear electric susceptibility tensor (measured at zero mechanical deformation).

The last term in Equation 3-83 represents the inverse electrostrictive effect.

The fourth order tensor Q can be effectively represented by a 6-by-6 coupling matrix. Further simplification due to material symmetry is possible in most cases. Thus, for cubic crystal material, the coupling matrix can be characterized by three independent components: Q11, Q12, and Q44.

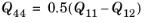
For an isotropic material, only two independent coefficients Q11 and Q12 are needed since . Two corresponding M-constants can be computed as

where χ0 denotes the only independent component of the electric susceptibility tensor.

For isotropic materials, the fourth order elasticity tensor C has only two independent components. The most common choice to represent those are by specifying the Young’s modulus EYM and Poisson’s ratio ν.

The following alternative electrostrictive parameters are defined in Ref. 1 for a linear isotropic material:

One more commonly used alternative definition is that introduced in Ref. 2. Using a1' and a2' for the constants used in Ref. 2, one has a1' = a1 − a2 and a2' = a2.

The SI units for different electrostrictive parameters are summarized in Table 3-6.