You are viewing the documentation for an older COMSOL version. The latest version is
available here.
Let r be the undeformed shell midsurface position,
ξi be element local (possibly nonorthogonal) coordinates with origin in the shell midsurface, and
n be the normal to the undeformed midsurface. The thickness of the shell is
d, which can vary over the element. The local coordinates
ξ1 and
ξ2 follow the midsurface, and
ξ3 is the coordinate in the normal direction. The normal coordinate has a value of
−d/2 on the bottom side of the element, and
+d/2 on the top side.
The position of the deformed midsurface is r + u, and the normal after deformation is
n + a. To keep the normal a unit vector requires that
(5-1)
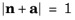
The vectors r,
u,
n, and
a are interpolated by the
nth-order Lagrange basis functions. The basic assumption is that the position of a point within the shell after deformation has a linear dependence of the thickness coordinate, and thus is
The indices α and
β range from 1 to 2. The transverse shear strains in local covariant components are
In a geometrically linear analysis, the nonlinear terms (products between u,
a, and their derivatives) disappear. In all study types, the contributions from the parts
καβ and
ωα are ignored. They are small unless the element has an extremely high ratio between thickness and radius of curvature, in which case the errors from using shell theory are large anyway.
|
|
Note that ζα here is a strain component, not to be confused with the local coordinate in the normal direction or offset.
|
where rR is the position of the meshed
reference surface and
ζo is the offset distance.
where t is the tangent to the edge. For an internal edge, it is possible that there is a discontinuity in thickness or offset. In such a case, the line scale factor will be an average. Edge conditions are not well defined in such situations because the position of the midsurface can be discontinuous. In practice, errors caused by such effects are small.
The MITC formulation (Ref. 1) does not take the strain components directly from the shape functions of the element. Instead, meticulously selected interpolation functions are selected for the individual strain components. The values of the interpolated strains are then at selected points in the element tied to the value that would be computed from the shape functions. The interpolation functions and tying points are specific to each element shape and order.
(5-2)
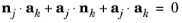
where the values or j and
k range over the number of shells elements with different normals. The third term in
Equation 5-2 is relevant only in a large deformation analysis because it is nonlinear. A special case occurs when two adjacent boundaries are parallel but their normal vectors have opposite directions. In this case the special constraint
All functions of ζ are assumed to be of the form
ζn. Odd powers will integrate to zero, so typically the through-thickness integration will give factors
d (for the case
n = 0) and
d3/12 (for the case
n = 2). The thickness
d can be a function of the position.
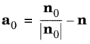
where Ω0 is the vector of prescribed nodal rotations. This relation is fully defined only when all three components of
Ω0 are given. It is also possible to prescribe only one or two of the components of
Ω0, while leaving the remaining components free. Because it has no relevance to prescribe the rotation about the normal direction of the shell, it is only possible prescribe individual rotations in a shell local system. In this case, the result becomes one or two constraint relations between the components of
a0. The directions are the edge local coordinate system where
t1 is the tangent to the edge and
t2 is perpendicular and inward from the edge, in the plane of the shell. These constraints are formulated as
Here Ω0i is the prescribed rotation around the axis
ti.
where R is a standard rotation matrix, representing the finite rotation about the given rotation vector.
for the antisymmetry case. Here t1 and
t2 are two perpendicular directions in the plane of the shell.
When applied to an edge, there is a local coordinate system where t1 is the tangent to the edge, and
t2 is perpendicular and in the plane of the shell. The assumption is then that
t2 is the normal to the symmetry or antisymmetry plane. The constraints are
In axisymmetric models, the only possible symmetry plane is the one having the Z-axis as normal. In this case, you can use the
Symmetry Plane boundary condition. The imposed constraint is
where the forces (F) and moments (
M) can be distributed over a boundary or an edge or concentrated in a point. The contribution from the normal vector displacement
a is only included in a geometrically nonlinear analysis. Loads are always referred to the midsurface of the element. In the special case of a follower load, defined by its pressure
p, the force intensity is
Each part of the covariant strain (γαβ,
χαβ,
ζα) is transformed separately. They correspond to membrane, bending, and shear action, respectively, and it is thus possible to separate the stresses from each of these actions. The membrane stress is defined as
where D is the plane stress constitutive matrix,
Ni are the initial membrane forces, and
γi the initial membrane strains. The influence of thermal strains is included through the midsurface temperature
Tm, and the hygroscopic swelling through the midsurface moisture concentration,
cm. The membrane stress can be considered as the stress at the midsurface, or as the average through the thickness.
where χi is the initial value of the bending part of the strain tensor (actually: the curvature), and
Mi are the initial bending and twisting moments.
ΔT is the temperature difference between the top and bottom surface of the shell, and
Δcmo is the difference in moisture concentration between the top and bottom. The bending stress is the stress at the top surface of the shell if no membrane stress is present.
where G represent the transverse shear moduli,
ζi is the initial average shear strain, and
Qi are the initial transverse shear forces. The correction factor
5/6 ensures that the stresses are averaged so that they correspond to the ratio between shear force and thickness. The corresponding strains
ζ and
ζi are averaged in an energy sense.
where z is a parameter ranging from
−1 (bottom surface) to
+1 (top surface). The computation of the shear stress at a certain level in the element uses the following analytical parabolic stress distribution:
If a Boundary System is selected, then the orientation of the shell local system is fully defined by the boundary system. When using a boundary system, it also possible to control the orientation of the shell normal by selecting the
Reverse normal direction check box.
1. The local z direction ezl is the positive geometry normal of the shell surface.
2. The local x direction exl is the projection of the first direction in the material coordinate system (
ex1) on the shell surface
This projection cannot be performed if ex1 is normal to the shell. In that case, the second axis
ex2 of the material system instead defines
exl using the same procedure. Thus, if
|
•
|
For shells in the XY-plane, and for plates, the global and local directions coincide by default.
|
|
•
|
The first direction (xl) is along the edge. This direction can be visualized by selecting the Show edge directions arrows check box in the View settings.
|
|
•
|
The third direction (zl) is the same as the shell normal direction. The shell normal direction can be visualized in the default plot named Undeformed geometry, or by adding a Coordinate System Surface plot and selecting the Shell, Local System.
|
|
•
|
The second direction (yl) is in the plane of the shell and orthogonal to the edge. It is formed by the cross product of zl and xl; yl = zl × xl.
|
When an edge is shared between two or more boundaries, the directions may not always be unique. It is then possible to use the control Face Defining the Local Orientations to select from which boundary the normal direction
zl should be picked. The default is
Use face with lowest number.
If the geometry selection contains several edges, the only available option is Use face with lowest number, since the list of adjacent boundaries would then be different for each edge. For each edge in the selection, the face with the lowest number attached to that edge is then used for the definition of the normal orientation.
For visualization and results evaluation, predefined variables include all nonzero stress and strain tensor components, principal stresses and
principal strains, in-plane and out-of-plane forces, moments, and von Mises and
Tresca equivalent stresses. It is possible to evaluate the stress and strain tensor components and equivalent stresses at an arbitrary distance from the midsurface. The parameter
zshell (variable name
shell.z) is found in, for example, the
Parameters table of the
Settings window of a surface plot. It can be set to a value from
−1 (downside) to
+1 (upside). A value of 0 means the midsurface of the shell. The default value is given in the
Default through-thickness result location section of the Shell interface.
The Shell dataset is tailored for display of results computed in the Shell interface. The purpose is to simultaneously show results on the top and bottom surfaces of the shell with a separation which matches the physics thickness. A Shell dataset with appropriate settings is generated together with the default plots, and some of the default plots make use of it.
The inertial properties mass (m) and moment of inertia tensor (
I)
of a rigid shell take the finite thickness into account. They are computed as:
where E3 and
XM are the identity matrix and the center of mass of the rigid domain, respectively. The last term in
I is accounting for the finite thickness, and there the fact that
nT ⋅ n = 1 has been used.
|
•
|
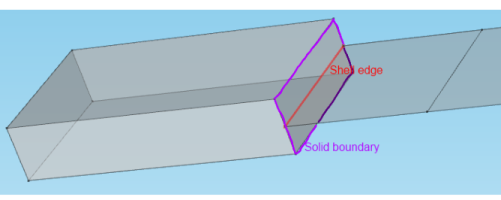
Type 1 connection: The shell connects to the solid in a thin region (having the same thickness as the shell), so that shell theory is valid on both sides. This connection is the most important from the application point of view and the most difficult to create manually.
|
|
•
|
Type 2 connection: The tangent plane to the shell is perpendicular to the face of a “thick” solid, in which case the physics of the connection can, at best, be approximate.
|
Figure 5-2 illustrates the first two cases. The shell edge can be part of the definition of the solid but there is no assumption about that.
|
•
|
x′ is the outward normal to the solid boundary
|
|
•
|
z′ is along the shell normal
|
|
•
|
y′ is the tangent to the shell edge, directed so that x′- y′- z′ form a right-hand system
|
where the subscripts sld and
sh represent “solid” and “shell”, respectively, and
a′ is the displacement of the shell normal, represented in the local directions.
Note that as the K1 term is related to membrane action, it cannot contribute to the transverse shear stress. Since the derivative in the
x′ direction cannot be controlled by a condition on the boundary, it is necessary to make an assumption about
u′(
z′). An integration with respect to
z′ gives
This shows that a third power of z′ is required in order to be able to represent the correct shear strain contribution.
Here qu,
qw1, and
qw2 are the new dependent variables defined on the shell edge. They are dimensionless, due to the multiplication with the shell thickness,
d. The constants
ku = 3/5 and
kw2 = 1/5 are explained below. The variable
qw1 is proportional to the membrane axial strain, the variable
qw2 is proportional to the bending strain, and the variable
qu is proportional to the transverse shear strain. Since these variables are directly related to strains, the shape function order used is one order lower than for the displacements.
If no extra equations defining qu,
qw1, and
qw2 are introduced, these variables try to adapt to proper values through the reaction forces on the solid. The reaction force for
u′ is the traction
σx′ and the reaction force for
w′ is the traction
τx′z′. When taking the variation of the new dependent variables, these enforce the following constraints:
The equation with qw1 is trivially fulfilled because the shear stress is an even function of
z′. Inserting the known stress distributions gives equations that can be solved for
ku and
kw2.
(5-3)
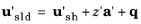
The fact that az′ = 0 has been used when formulating
Equation 5-3.
The only coordinate value needed is actually z′. For the other two coordinates, only the direction is important. The coordinate in the normal direction can be computed as
This definition of z′ assumes that the thickness of the solid does not change significantly. Under geometric nonlinearity, the computation should be based on the current geometry.
Let Φ be the matrix that transforms displacements from the global system to the local system:
where N is the undeformed shell normal (
shell.an) and
tl is the shell edge tangent (
shell.tle). The coefficient
s is either 1 or
−1, and is selected so that the
x′ direction coincides with the outward normal of the solid.
where ζ is a distance from the solid to the shell. The right-hand side is mapped from the shell to the solid using an extrusion operator. The default is that
ζ is half the shell thickness, but you can also use the geometrical distance between the boundaries, or a user-defined distance.
where n is the normal to the shell. The rotation vector in the beam can be expressed in the shell degrees of freedom as
The definitions of n,
t1, and
t2 may, however, be discontinuous over a shell edge. For this reason, the constraint is formed using values from one boundary only if several boundaries share the edge. Another complication arises when the edge is a
fold line, that is when the boundaries that meet do not have a common normal direction. On a fold line all three rotational degrees of freedom do exist in the shell and should then be connected to the corresponding degrees of freedom in the shell. In this case, also a third rotational constraint is formed.
This coupling is intended for the case when the beam is not in the same plane as the boundary modeled by shell theory. This case is called Shell boundaries to beam points in the
Shell-Beam Connection node. Physically, this can be seen as a beam with one end welded to a plate. In order to get a correct stiffness representation of such a connection, it is necessary that the beam is connected to an area of the shell which is similar to the actual physical width of the beam. The connected area on the shell does not have to fit a boundary in the geometry. It is however necessary that the mesh size is such that there are at least three nodes within the connected area.
