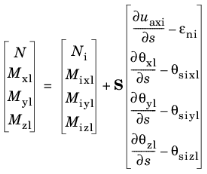Theory for Section Stiffness

The Section Stiffness node in the Beam interface allows modeling of beams with non-homogeneous cross sections by, instead of geometrical and material properties, directly entering values for the stiffness matrix S.

For a 3D Euler-Bernoulli beam, the relationship between the section forces and the deformation of the beam is given by

(8-1)

including initial normal force Ni; moments Mixl, Miyl, and Mizl; normal strain εi; and curvatures θsixl, θsiyl, and θsizl. Here, S is a 4 by 4 symmetric matrix. For a homogeneous prismatic beam with isotropic material properties, it is defined as

For a 2D Euler-Bernoulli beam, out-of-plane moments are zero, and Equation 8-1 thus simplifies to

with S now being a 2 by 2 symmetric matrix.

For a 3D Timoshenko beam, the relationship between the section forces and the deformation of the beam is given by

(8-2)

with S being a 6 by 6 symmetric matrix. The equation now also includes the initial shear forces Tiyl and Tizl as well as the initial shear strains γiyl and γizl.

For a 2D Timoshenko beam, out-of-plane forces and moments are zero, and Equation 8-2 thus simplifies to

with S now being a 3 by 3 symmetric matrix.

Using the section forces, the virtual work for the beam becomes

where only the relevant terms are kept, depending on the beam formulation and the spatial dimension.