Use the Medium Properties node to specify the refractive index of the medium. An instance of this feature is created by default, including all of the selected domains for the physics interface. For the region outside the geometry and for any domains not included in the physics interface selection, the refractive index is instead controlled by the
Optical dispersion model in the physics interface
Material Properties of Exterior and Unmeshed Domains section.
For example, suppose that a model contains two lenses consisting of two different glasses, and that the first glass is defined using Sellmeier coefficients whereas the second glass is defined using
Schott coefficients. Then selecting
Get dispersion model from material will automatically express the refractive index using the
Sellmeier equation in the first lens and the
Schott (polynomial) equation in the second. An alternative way to use different optical dispersion models in different domains is to use more than one instance of the
Medium Properties node and select the dispersion models manually.
The coefficients for each of these dispersion models are taken From material by default. Alternatively,
User defined coefficients may be entered.
Similar to the option Specify relative refractive index, most of the built-in optical dispersion models define the refractive index relative to air, and therefore they all require a reference temperature and pressure to be specified. The only exception is the
Temperature-dependent Sellmeier, in which the refractive index is assumed to be absolute, such that
n = 1 is the refractive index of an ideal vacuum. To use any other optical dispersion model to define an absolute index, set the reference pressure to zero.
Using the Temperature-dependent Sellmeier model also disables the settings for selecting a
Thermo-optic dispersion model (see the following subsection).
If ray intensity or power is computed, specify the Refractive index, imaginary part k (dimensionless). By default the
Refractive index, imaginary part k uses values
From material. For
User defined enter a value or expression. The convention followed by the Geometrical Optics interface is that the imaginary part of the refractive index is negative in absorbing media. A positive value indicates a gain medium in which the intensity increases as the ray propagates.
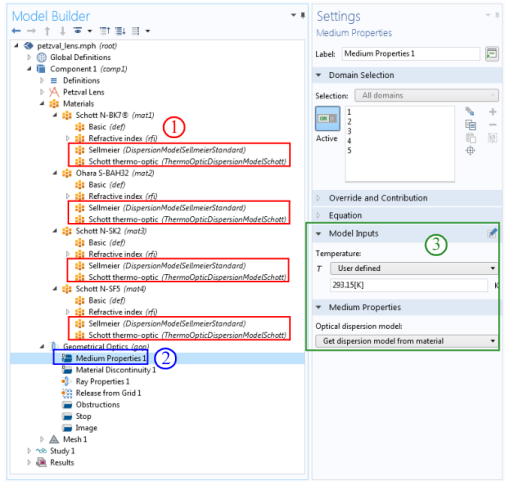
The option Get dispersion model from material is unique because it allows a single
Medium Properties node to detect different optical dispersion models from a large number of different materials having different domain selections. For example, the materials used in the Petzval Lens tutorial are shown in
Figure 3-2 below. To automatically detect the optical dispersion models of the loaded glasses, take the following steps: