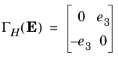The divergence on ΓE(H) is applied row-wise. The conductivity and permittivity tensors
σ and
εr represent in-plane material properties, while the relative permeability
μr is an out-of-plane scalar property.
The default Lax-Friedrichs flux parameters are τE = 1/(2Z) for Ampère’s law, and the scalar
τH = Z/2 for Faraday’s law, where
Z is the impedance of a vacuum.
The divergence of ΓH(E) is applied row-wise. The tensor of relative permeability
μr represents in-plane material properties, while the relative permittivity
εr and conductivity
σ are out-of-plane scalar properties.
The default Lax-Friedrichs flux parameters are τE = 1/(2Z) for Ampère’s law, and two scalar
τH = Z/2 for Faraday’s law, where
Z is the impedance of a vacuum.
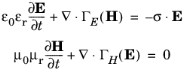
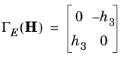 and
and