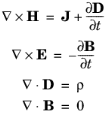The Equations
Maxwell’s equations are a set of equations, written in differential or integral form, stating the relationships between the fundamental electromagnetic quantities. These quantities are the:
•
Electric field intensity E
•
Electric displacement or electric flux density D
•
Magnetic field intensity H
•
Magnetic flux density B
•
Current density J
•
Electric charge density ρ
For general time-varying fields, the differential form of Maxwell’s equations can be written as
(4-10)
The first two equations are also called Maxwell-Ampère’s law and Faraday’s law, respectively. Equation three and four are two forms of Gauss’ law, the electric and magnetic form, respectively.
Constitutive Relations
To obtain a closed system of equations, the constitutive relations describing the macroscopic properties of the medium are included. These are given as
(4-11)
Here ε0 is the permittivity of a vacuum, μ0 is the permeability of a vacuum, and σ the electric conductivity of the medium. In the SI system, the permeability of a vacuum is chosen to be 4π·10−7 H/m. The velocity of an electromagnetic wave in a vacuum is given as c0 and the permittivity of a vacuum is derived from the relation
The electric polarization vector P describes how the material is polarized when an electric field E is present. It can be interpreted as the volume density of electric dipole moments. P is generally a function of E. Some materials might have a nonzero P also when there is no electric field present.
The magnetization vector M similarly describes how the material is magnetized when a magnetic field H is present. It can be interpreted as the volume density of magnetic dipole moments. M is generally a function of H. Permanent magnets, for example, have a nonzero M also when there is no magnetic field present.
To get a wave equation for the E field, for example, take the curl of the second equation in Equation 4-10 (previously divided by μ0), and insert it into the time derivative of the first row in Equation 4-10
this is referred as curl-curl formulation in the literature (second order time derivatives and second order space derivatives).
Linear Materials
In the simplest case linear materials, the polarization is directly proportional to the electric field, that is
and
where χe is the electric susceptibility (which can be a scalar or a second-rank tensor). Similarly, the magnetization is directly proportional to the magnetic field, or
and
where χm is the magnetic susceptibility.
As a consequence, for linear materials, the constitutive relations in Equation 4-11 can be written as
Here, ε = ε0εr and μ = μ0μr are the permittivity and permeability of the material. The relative permittivity εr and the relative permeability μr are usually scalar properties but these can be second-rank symmetric (Hermitian) tensors for a general anisotropic material.
For general time-varying fields, Maxwell’s equations in linear materials described in Equation 4-10 can be simplified to Maxwell-Ampère’s law and Faraday’s law:
(4-12)
The electric conductivity σ can also be a scalar or a second-rank tensor. Another important assumption is that the relative permittivity εr, the relative permeability μr and the electric conductivity σ might change with position and orientation (inhomogeneous or anisotropic materials) but not with time.
First-order Implementation of Maxwell’s Equations
In order to accommodate Maxwell’s equations in the coefficients for the Wave Form PDE interface in the form
the curl of a vector is written in divergence form as
(4-13)
where the divergence is applied on each row of the flux Γ(u).
Maxwell’s equations in 3D
are then accommodated to the Wave Form PDE as
with the “mass” coefficients
and
the “flux” terms
and
and the “source” term f = −σE.
The Lax-Friedrichs Flux Parameters
When using SI units (or other) for the electromagnetic fields and material properties, the Lax-Friedrichs flux parameter is not dimensionless and must have units of τE = 1/(2Z) for Ampère’s law and τH = Z/2 for Faraday’s law, where Z is the impedance of the medium.