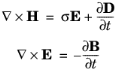The Wave Equations node is the main node for the Electromagnetic Waves, Time Explicit interface. The governing transient equations can be written in the form

with the constitutive relations B = μ0μrH and D = ε0εrE, which reads

The default Relative permittivity εr (dimensionless), Relative permeability μr (dimensionless), and Electrical conductivity σ (SI unit: S/m) take values From material. For User defined select Isotropic, Diagonal, Symmetric, or Full and enter values or expressions in the field or matrix.

The filter provides higher-order smoothing of nodal discontinuous Galerkin formulations and is intended to be used for absorbing layers, but you can also use it to stabilize linear wave problems with highly varying coefficients. The filter is constructed by transforming the solution (in each global time step) to an orthogonal polynomial representation, multiplying with a damping factor and then transforming back to the (Lagrange) nodal basis. Select the Activate check box to use this filter.

where V is a Vandermonde matrix induced by the node points, and Λ is a diagonal matrix with the exponential damping factors on the diagonal:

and Np is the basis function and im the polynomial order for coefficient m. α (default value: 36), ηc (default value: 1), and s (default value: 3) are the filter parameters that you specify in the corresponding text fields. The damping is derived from a spatial dissipation operator of order 2s. For s = 1, you obtain a damping that is related to the classical 2nd-order Laplacian. Higher order (larger s) gives less damping for the lower-order polynomial coefficients (a more pronounced low-pass filter), while keeping the damping property for the highest values of η, which is controlled by α. The default values 36 for a correspond to maximal damping for η = 1. It is important to realize that the effect of the filter is influenced by how much of the solution (energy) is represented by the higher-order polynomial coefficients. For a well resolved solution this is a smaller part than for a poorly resolved solution. The effect is stronger for poorly resolved solutions than for well resolved ones. This is one of the reasons why this filter is useful in an absorbing layer where the energy is transferred to the higher-order coefficients through a coordinate transformation. See Ref. 1 (Chapter 5) for more information.

α must be positive; α = 0 means no dissipation, and the maximum value is related to the machine precision, −log(ε), which is approximately 36. ηc should be between 0 and 1, where ηc = 0 means maximum filtering, and ηc = 1 means no filtering, even if filtering is active.

When using Absorbing Layer features, add an additional Wave Equations feature for the corresponding domain selection. Select the Activate check box and add filter parameters. An example of a filter parameter combination that can be used for a Wave Equations feature active on an Absorbing Layer domain selection is α = 0.1, ηc = 0.01, and s = 2. However, other combinations could work better, depending on the particular application.