Evaluating the sensitivity of a scalar-valued objective function Q(ξ) with respect to the control variables, ξ, at a specific point, ξ0, can be rephrased as the problem of calculating the derivative ∂Q/∂ξ at ξ = ξ0. In the context of a multiphysics model, Q is usually not an explicit expression in the control variables ξ alone. Rather, Q(u(ξ), ξ) is also a function of the solution variables u, which are in turn implicitly functions of ξ.

The multiphysics problem is a PDE, which after discretization is represented as a system of equations L(u(ξ), ξ) = 0. If the PDE has a unique solution u = L-1(ξ), the sensitivity problem can be informally rewritten using the chain rule as that of finding

The first term, which is an explicit partial derivative of the objective function with respect to the control variables, is easy to compute using symbolic differentiation. The second term is more difficult. Assuming that the PDE solution has N degrees of freedom and that there are n control variables ξi, ∂Q/∂u is an N-by-1 matrix, ∂u/∂L is an N-by-N matrix (because L−1 is unique), and ∂L/∂ξ is an N-by-n matrix.

The first and last factors, ∂Q/∂u and ∂L/∂ξ, can be computed directly using symbolic differentiation. The key to evaluating the complete expression lies in noting that the middle factor can be computed as ∂u/∂L = (∂L/∂u)−1 and that ∂L/∂u is the PDE Jacobian at the solution point:

Actually evaluating the inverse of the N-by-N Jacobian matrix is too expensive. In order to avoid that step, an auxiliary linear problem can be introduced. This can be done in two different ways, each requiring at least one additional linear solution step (see Forward Sensitivity Methods and Adjoint Sensitivity Method below).

Assume that the Jacobian 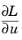in Equation 2-4 above is incomplete and denote it by .

Then, the solution to the system in Equation 2-5 is approximated iteratively by

where n is the iteration number.

If the previous algorithm does not converge (that is, the estimated error is larger than the given tolerance), the sensitivity computations are repeated using the incomplete Jacobian and the warning Jacobian is incomplete. No convergence when attempting to use the complete Jacobian is written.

If the assemble of the complete Jacobian fails, the incomplete Jacobian is used and the warning Unable to assemble the complete Jacobian. Using incomplete Jacobian for sensitivity analysis is written.

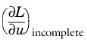
To use the forward sensitivity methods, introduce the N-by-n matrix of solution sensitivities

These can be evaluated by solving n linear systems of equations

using the same Jacobian ∂L/∂u, evaluated at u(ξ0). Inserting the result into Equation 2-4, the desired sensitivities can be easily computed as

To use the adjoint sensitivity method, introduce instead the N-by-1 adjoint solution u∗, which is defined as

Multiplying this relation from the right with the PDE Jacobian ∂L/∂u and transposing leads to a single linear system of equations