PDE-Constrained Optimization
In multiphysics modeling, it is often desirable to let control variables parameterize the problem and seek to optimize a function of the PDE solution. The objective function is therefore a function of both the control variables and the PDE solution, which is in turn a function of the control variables. The multiphysics problem is a PDE, which after discretization is represented as a system of equations L(u(ξ), ξ) = 0, where u is the PDE solution and ξ the control variables.
The complete PDE-constrained optimization problem to be solved by one of the optimization algorithms in the Optimization Module adds the PDE problem as an equality constraint to the general optimization problem:
(2-2)
It is advantageous to separate those constraints in G that are defined as explicit expressions of ξ only (design constraints) from those that mix u and ξ (performance constraints). The former group can further be divided into simple bounds, which set a lower and upper limit directly on the control variables, and constraints on general expressions of the control variables. Hence, the general constraint formulation lb ≤ G(u(ξ), ξ) ≤ ub above is replaced by three classes of constraints:
and the optimization problem in Equation 2-2 can be written as
(2-3)
This is the general form of the optimization problem considered in the Optimization Module. Control variables ξ can be either global model parameters converted into control variables in the Optimization study step or control variable fields set up in an Optimization interface. You specify the objective function and the constraints in the form of expressions of ξ and u. The relation between u and ξ, which is a system of equations written here compactly as L(u, ξ) = 0, is given by the multiphysics model.
Specification of the Objective Function
The objective function is, in general, a sum of a number of terms:
where n is the space dimension of the multiphysics model and the different contributions in the sum above are defined as follows:
•
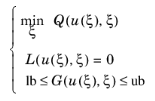
Qglobal is the global contribution to the objective function Q. It is given as one or more general global expressions, either in an Optimization study step or in a Global Objective node under an Optimization interface.
•
Qprobe is a probe contribution to the objective function Q. It is a probe objective so its definition is restricted to a point on a given geometrical entity. You specify the probe point used for the point evaluation explicitly in a Probe Objective node under an Optimization interface.
•
Qint,k is an integral contribution to the objective function Q. It is an integral objective so its definition is restricted to a set of geometric entities of the same dimension. Use an Integral Objective node under an Optimization interface to specify an integrand and a select a set of domains, boundaries, edges or points over which to integrate. For a point selection, the integration reduces to a summation.
Several global, probe, and integral contributions can be defined in separate nodes under an Optimization interface. In such cases, the total global, probe, and integral contribution is given as the sum of the contributions. If you specify one or more objectives directly in the Optimization study step, these are also added to the sum.
Specification of Constraints
The full nonlinear set of constraints lb ≤ G(u(ξ), ξ) ≤ ub in the general PDE-constrained optimization problem, Equation 2-2, are separated into three groups:
The first row above contains the general implicit constraints, or performance constraints in the case of a design problem. These are given in terms of expressions involving both the solution variables u and control variables ξ. The second row constitutes the explicit constraints — or design constraints — which are those constraints given by explicit expressions only in the control variables ξ. The last row contains the control variable bounds
The reason for this subdivision is computational. Each evaluation of an implicit constraint requires an up-to-date solution of the multiphysics solution u. The gradient-based optimization methods also require a complete sensitivity evaluation, which is computationally demanding; see Choosing a Sensitivity Method in the COMSOL Multiphysics Reference Manual.
Explicit constraints, in contrast, can be computed without updating the multiphysics solution. They can, however, be nonlinear, making it difficult for the optimization methods to follow an active constraint. Control variable bounds are the least expensive to handle, since when active, the optimization solver can essentially just exclude the corresponding control variable.
The Optimization interface differentiates between the following constraints (in the description that follows, n denotes the dimension of the multiphysics model): control variable bounds, pointwise inequality constraints, integral inequality constraints, and global inequality constraints, each of which are described below.
•
Bounds or control variable bounds are inequality constraints setting lower and upper bounds directly on each control variable degree of freedom. Hence, bound constraints correspond to constraints of the form lb ≤ ξ ≤ ub. They are handled efficiently by all solvers that support them and in many cases improve solver stability and efficiency.
•
Pointwise inequality constraints are inequality constraints involving an explicit expression in terms of the control variables. This type of constraint sets lower and upper bounds on the expression for node points in a set of geometric entities of the same dimension.
•
Global inequality constraints set upper and lower bounds on a general global expression, possibly involving both the control variables and the PDE solution. Apart from the specification of bounds, a global inequality constraint is identical to a Global Objective.
•
Integral inequality constraints set upper and lower bounds on an integral of an expression, possibly involving the PDE solution and control variables, over a set of geometric entities of the same dimension. For integral inequality constraints on points, the integration reduces to a summation.
Global inequality constraints and integral inequality constraints are structurally similar to the objective function and equally expensive to evaluate.