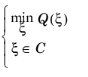Optimization Problem Formulation

The Optimization Module is built around a general single-objective minimization problem formulation. The Optimization Study node transforms maximization as well as multiobjective minimax and maximin problems internally to the canonical minimization form.

The General Optimization Problem

The most general formulation of an optimization problem can be written as

(2-1)

Here, the control variables are denoted by ξ, the scalar-valued objective function by Q, and the feasible set is denoted by C. Assuming sufficient continuity, the feasible set can be expressed as a set of — possibly very nonlinear — inequality constraints

where G is a vector-valued function (G is scalar-valued in case of a single constraint).


	For vectorial quantities, the inequality defining C is to be interpreted component-wise, and lb and ub are the corresponding vectors containing the upper and lower bounds, respectively.

Classical Optimization

In classical optimization, Q and G are given explicitly as closed-form expressions of the control variables ξ. However, design problems and parameter estimation problems often result in objective functions Q and constraints G that are not explicitly expressible as closed-form expressions of the control variables ξ.