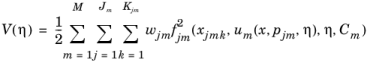where M is the number of series (measurement series), Jm is the number of measurements, and Kjm is the number of points. The variable x is the space coordinates, η are the parameters for which the cost function should be minimized and um(x, p, η) solves a given PDE or ODE. The variable p is time if the PDE or ODE is time-dependent but it can also represent any parameter when the forward problem is stationary. The functions wjm are weight functions, and fjm represent the difference between some model function gjm and some measured data gjmk; that is, fjm can be written as

The Levenberg-Marquardt algorithm as implemented in the Optimization Module relies on two fundamental ideas: evaluation of an approximate Hessian and regularization of the Hessian approximation. The special structure of least-squares objective functions allows cheap evaluation of an approximate Hessian (matrix of second derivatives), which can in principle be used directly in a Newton iteration. However, least-squares problems are also often ill-conditioned, making the full Newton process unstable. Therefore, the Hessian is modified using a regularization parameter to guarantee its positive definiteness. This parameter is updated between iterations, based on the success or failure of the previous step. For further details, see Ref. 10.