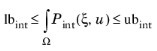Integral Inequality Constraints (
Point Sum Inequality Constraints on points) specify bounds on the value of the integral of an expression
Pint(ξ,u) taken over a selected set of geometric entities of the same dimension,
Ω:
Enter a Constraint expression that is integrated over the domain in the integral inequality constraint.
Specify the settings for the Quadrature used to numerically evaluate the integral in the integral objective: the integration order (default: 4) in the
Integration order field and the frame to integrate on (default: the spatial frame), which is selected from the
Integrate on frame list.
By default, the Lower bound and
Upper bound check boxes are selected to activate the required bounds. To specify equality constraints, simply make sure the upper and lower bounds have the same value.