
|
|
1
|
|
2
|
In the Select Physics tree, select Optics>Wave Optics>Electromagnetic Waves, Frequency Domain (ewfd).
|
|
3
|
Click Add.
|
|
4
|
Click Add.
|
|
5
|
Click
|
|
6
|
|
7
|
Click
|
|
1
|
|
2
|
|
3
|
|
4
|
Browse to the model’s Application Libraries folder and double-click the file second_harmonic_generation_frequency_domain_parameters.txt.
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
Click to expand the Layers section. In the table, enter the following settings:
|
|
6
|
|
7
|
|
8
|
|
1
|
In the Model Builder window, expand the Component 1 (comp1)>Definitions>View 1 node, then click Axis.
|
|
2
|
|
3
|
|
4
|
Click
|
|
5
|
|
1
|
In the Model Builder window, under Component 1 (comp1) right-click Materials and choose Blank Material.
|
|
2
|
|
1
|
In the Model Builder window, under Component 1 (comp1) click Electromagnetic Waves, Frequency Domain (ewfd).
|
|
2
|
In the Settings window for Electromagnetic Waves, Frequency Domain, type Fundamental in the Label text field.
|
|
3
|
|
4
|
Locate the Components section. From the Electric field components solved for list, choose In-plane vector, as only the in-plane polarization will be included in the simulation.
|
|
1
|
|
3
|
|
4
|
|
1
|
|
3
|
In the Settings window for Scattering Boundary Condition, locate the Scattering Boundary Condition section.
|
|
4
|
|
5
|
|
1
|
|
1
|
In the Model Builder window, under Component 1 (comp1) click Electromagnetic Waves, Frequency Domain 2 (ewfd2).
|
|
2
|
In the Settings window for Electromagnetic Waves, Frequency Domain, type Second Harmonic in the Label text field.
|
|
3
|
Locate the Components section. From the Electric field components solved for list, choose In-plane vector.
|
|
4
|
|
5
|
|
1
|
|
3
|
|
4
|
|
1
|
|
1
|
|
2
|
|
1
|
|
2
|
Click the Custom button.
|
|
3
|
|
4
|
|
1
|
In the Model Builder window, under Component 1 (comp1) right-click Definitions and choose Variables.
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
1
|
|
2
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|
|
9
|
|
1
|
|
2
|
|
3
|
|
4
|
Locate the Legends section. In the table, enter the following settings:
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
1
|
|
2
|
|
4
|
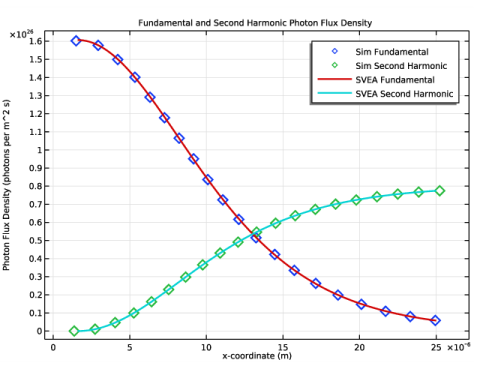
Locate the y-Axis Data section. In the Expression text field, type ewfd1.Ey*conj(ewfd1.Ey)/(2*Z0_const)/hbar_const/(2*pi*ewfd1.freq).
|
|
5
|
|
6
|
|
7
|
Locate the Coloring and Style section. Find the Line style subsection. From the Line list, choose None.
|
|
8
|
|
9
|
|
10
|
|
11
|
|
12
|
|
1
|
|
2
|
|
3
|
Locate the y-Axis Data section. In the Expression text field, type ewfd2.Ey*conj(ewfd2.Ey)/(2*Z0_const)/hbar_const/(2*pi*ewfd2.freq).
|
|
4
|
Locate the Legends section. In the table, enter the following settings:
|
|
1
|
|
2
|
In the Settings window for Line Graph, type Slowly Varying Envelope Approximation (SVEA) Fundamental in the Label text field.
|
|
3
|
|
4
|
|
5
|
|
7
|
Locate the y-Axis Data section. In the Expression text field, type (sech(gamma*(x - offset)/2))^2*I1/hbar_const/(2*pi*ewfd1.freq).
|
|
8
|
Locate the Coloring and Style section. Find the Line style subsection. From the Line list, choose Solid.
|
|
9
|
|
10
|
|
11
|
Locate the Legends section. In the table, enter the following settings:
|
|
1
|
|
2
|
In the Settings window for Line Graph, type Slowly Varying Envelope Approximation (SVEA) Second Harmonic in the Label text field.
|
|
3
|
Locate the y-Axis Data section. In the Expression text field, type (tanh(gamma*(x - offset)/2))^2*I1/hbar_const/(2*pi*ewfd2.freq).
|
|
4
|
Locate the Legends section. In the table, enter the following settings:
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|