
|

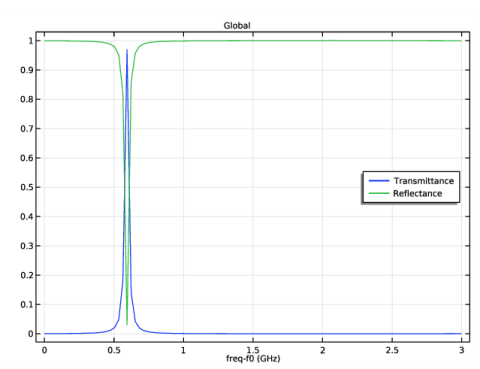

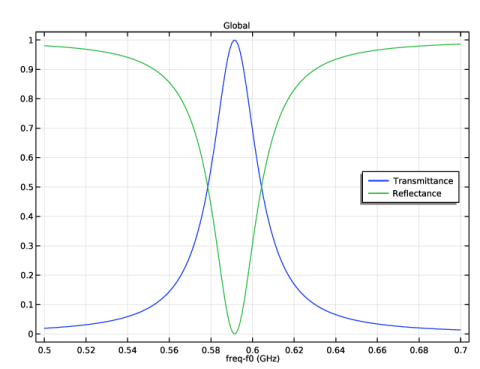
|
1
|
|
2
|
|
3
|
Click Add.
|
|
4
|
Click
|
|
5
|
|
6
|
Click
|
|
1
|
|
2
|
|
3
|
|
4
|
Browse to the model’s Application Libraries folder and double-click the file fabry_perot_resonator_geometry_parameters.txt.
|
|
1
|
|
2
|
|
3
|
|
4
|
Browse to the model’s Application Libraries folder and double-click the file fabry_perot_resonator_cavity_parameters.txt.
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
In the Model Builder window, expand the Component 1 (comp1)>Definitions>View 1 node, then click Axis.
|
|
2
|
|
3
|
|
4
|
Click
|
|
5
|
|
1
|
In the Model Builder window, under Component 1 (comp1) right-click Materials and choose Blank Material.
|
|
2
|
|
3
|
|
1
|
In the Model Builder window, under Component 1 (comp1) click Electromagnetic Waves, Beam Envelopes (ewbe).
|
|
2
|
|
3
|
From the Electric field components solved for list, choose Out-of-plane vector. This reduces the degrees of freedom for the model and restricts the solution to out-of-plane TE waves.
|
|
1
|
In the Physics toolbar, click
|
|
1
|
|
3
|
In the Settings window for Transition Boundary Condition, locate the Transition Boundary Condition section.
|
|
4
|
|
5
|
|
1
|
|
3
|
In the Settings window for Scattering Boundary Condition, locate the Scattering Boundary Condition section.
|
|
4
|
|
5
|
|
6
|
In the p0 text field, type l_in+l_cav/2, which places the focal plane for the Gaussian beam at the center of the cavity.
|
|
7
|
|
1
|
|
2
|
|
3
|
|
1
|
In the Physics toolbar, click
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
In the NT text field, type 60. This will create the mapped mesh with sixty elements over the wavefront.
|
|
4
|
In the NL text field, type 30. This will create the mapped mesh with thirty elements along the simulation domain. This will be sufficient to study the Fabry-Perot cavity.
|
|
5
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
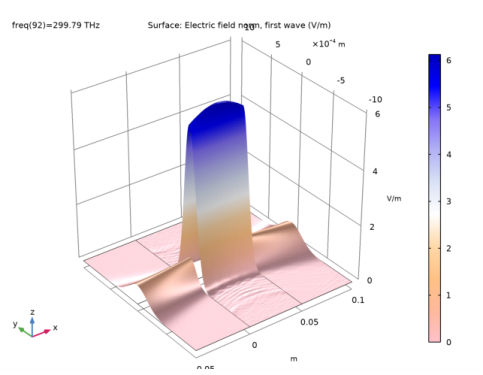
From the Parameter value (freq (THz)) list, choose 299.79 (21), which corresponds to the resonance frequency.
|
|
1
|
|
2
|
|
3
|
In the Expression text field, type ewbe.normE1 to display the norm of the electric field for the first wave.
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
In the Settings window for Arrow Surface, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1 (comp1)>Electromagnetic Waves, Beam Envelopes>Energy and power>ewbe.Poav1x,ewbe.Poav1y - Power flow, time-average, first wave.
|
|
3
|
Locate the Arrow Positioning section. Find the X grid points subsection. In the Points text field, type 10.
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
In the Expression text field, type ewbe.normE2 to display the norm of the electric field for the second wave.
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
In the Model Builder window, under Results>Electric Field (ewbe) right-click Arrow Surface 1 and choose Duplicate.
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
1
|
|
2
|
|
4
|
|
5
|
|
6
|
|
7
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
From the Parameter value (freq (THz)) list, choose 299.79 (92), which corresponds to the resonance frequency.
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
Click
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
4
|
|
5
|
|
6
|