
|

|
m/s2
|
||||
|
kg/m3
|
||||
|
m·s2/kg
|
10-8
|
10-8
|
||
|
m·s2/kg
|
4.4·10-10
|
4.4·10-10
|
||
|
8.25·10-5
|
5.83·10-5
|
|||
|
m-1
|
||||
|
1
|
|
2
|
In the Select Physics tree, select Fluid Flow>Porous Media and Subsurface Flow>Richards’ Equation (dl).
|
|
3
|
Click Add.
|
|
4
|
In the Select Physics tree, select Fluid Flow>Porous Media and Subsurface Flow>Richards’ Equation (dl).
|
|
5
|
Click Add.
|
|
6
|
Click
|
|
7
|
|
8
|
Click
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
Select the object c1 only.
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
5
|
|
1
|
In the Model Builder window, under Component 1 (comp1)>Richards’ Equation (dl) click Richards’ Equation Model 1.
|
|
2
|
|
3
|
|
4
|
Locate the Matrix Properties section. From the Permeability model list, choose Hydraulic conductivity.
|
|
5
|
|
6
|
Locate the Storage Model section. From the χf list, choose User defined. In the associated text field, type 4.4e-10.
|
|
7
|
|
8
|
|
9
|
|
10
|
|
11
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
3
|
|
4
|
|
1
|
In the Model Builder window, under Component 1 (comp1)>Richards’ Equation 2 (dl2) click Richards’ Equation Model 1.
|
|
2
|
|
3
|
|
4
|
Locate the Matrix Properties section. From the Permeability model list, choose Hydraulic conductivity.
|
|
5
|
|
6
|
Locate the Storage Model section. From the χf list, choose User defined. In the associated text field, type 4.4e-10.
|
|
7
|
|
8
|
|
9
|
|
10
|
|
11
|
|
12
|
|
13
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
5
|
|
6
|
|
7
|
|
8
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
In the Model Builder window, under Results>Effective Saturation right-click Line Graph 1 and choose Duplicate.
|
|
2
|
|
3
|
|
4
|
Click to expand the Coloring and Style section. Find the Line style subsection. From the Line list, choose Dashed.
|
|
5
|
|
6
|
Click to expand the Legends section.
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
3
|
|
5
|
Click
|
|
1
|
|
2
|
|
3
|
|
4
|
Locate the Expressions section. In the table, enter the following settings:
|
|
5
|
|
1
|
Go to the Table window.
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
Locate the Coloring and Style section. Find the Line style subsection. From the Line list, choose Dashed.
|
|
5
|
|
6
|
Locate the Legends section. In the table, enter the following settings:
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|
|
9
|
|
10
|
|
11
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
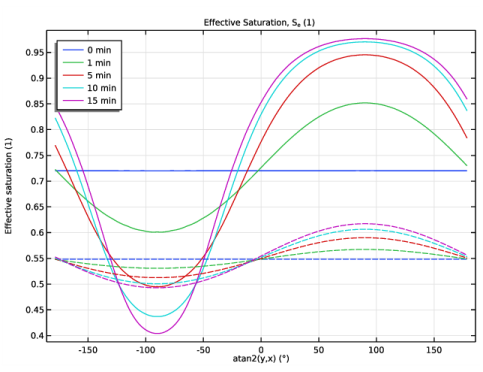
In the Settings window for 1D Plot Group, type Average effective saturation in the Label text field.
|
|
3
|
|
4
|
|
5
|
|
6
|
In the associated text field, type S<sub>e</sub>(1).
|
|
7
|