
|
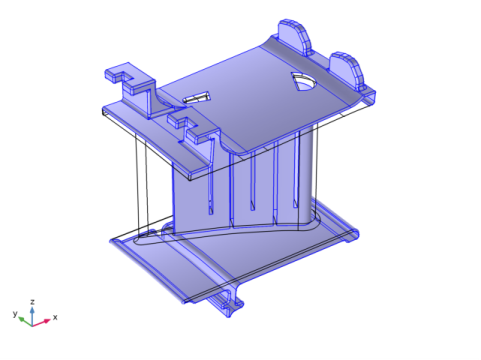
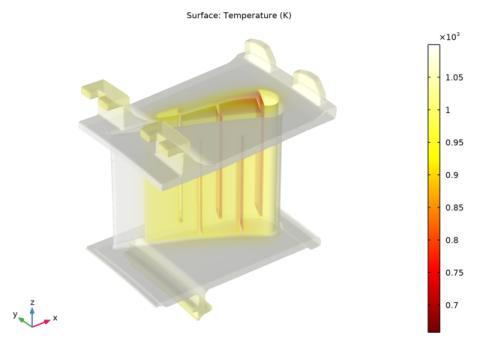

|
1
|
|
2
|
In the Select Physics tree, select Structural Mechanics>Thermal-Structure Interaction>Thermal Stress, Solid.
|
|
3
|
Click Add.
|
|
4
|
Click
|
|
5
|
|
6
|
Click
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
Click Browse.
|
|
4
|
Browse to the model’s Application Libraries folder and double-click the file turbine_stator.mphbin.
|
|
5
|
Click Import.
|
|
6
|
|
7
|
|
8
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
In the Paste Selection dialog box, type 222-225, 236, 261-266, 270-271, 278-279, 283-285, 292-305, 308-311, 313-314, 316, 321 in the Selection text field.
|
|
6
|
Click OK.
|
|
7
|
|
8
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
In the Paste Selection dialog box, type 3-4, 9, 12, 14, 16, 19-20, 22-24, 28-96, 98-117, 122-135, 138-162, 166-221, 223, 226-231, 239-260, 267-269, 272-277, 280-282, 322-444 in the Selection text field.
|
|
6
|
Click OK.
|
|
1
|
|
2
|
|
3
|
In the tree, select Material Library>Nickel Alloys>GTD111 DS>GTD111 DS [solid]>GTD111 DS [solid,longitudinal].
|
|
4
|
|
5
|
|
1
|
|
3
|
|
1
|
In the Model Builder window, expand the Component 1 (comp1)>Materials>GTD111 DS [solid,longitudinal] (mat1)>Young’s modulus and Poisson’s ratio (Enu) node, then click Piecewise (E_solid_longitudinal_1).
|
|
2
|
|
3
|
|
1
|
In the Model Builder window, under Component 1 (comp1)>Multiphysics click Thermal Expansion 1 (te1).
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
Find the Expression for remaining selection subsection. In the Volume reference temperature text field, type 300[K].
|
|
1
|
In the Model Builder window, under Component 1 (comp1)>Heat Transfer in Solids (ht) click Initial Values 1.
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|
|
9
|
|
10
|
|
1
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|
|
9
|
|
10
|
|
1
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|
|
9
|
|
10
|
|
1
|
|
1
|
|
3
|
|
4
|
From the list, choose Diagonal.
|
|
5
|
|
1
|
|
3
|
|
4
|
From the list, choose Diagonal.
|
|
5
|
|
1
|
|
3
|
|
4
|
From the list, choose Diagonal.
|
|
5
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
1
|
|
2
|
In the Settings window for Volume, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1 (comp1)>Solid Mechanics>Displacement>solid.disp - Displacement magnitude - m.
|
|
3
|
|
4
|
|
5
|