PDF
Channel Beam
Introduction
In the following example you build and solve a simple 3D beam model using the 3D Beam interface. This example calculates the deformation, section forces, and stresses in a cantilever beam, and compares the results with analytical solutions. The first few natural frequencies are also computed. The purpose of the example is twofold: It is a verification of the functionality of the beam element in COMSOL Multiphysics, and it explains in detail how to give input data and interpret results for a nontrivial cross section.
This example also illustrates how to use the Beam Cross Section interface to compute the beam section properties and evaluate the stress distribution within the beam cross section.
Model Definition
The physical geometry is displayed in Figure 1. The finite element idealization consists of a single line.
Figure 1: The physical geometry.
The cross section with its local coordinate system is shown in Figure 2. The height of the cross section is 50 mm and the width is 25 mm. The thickness of the flanges is 6 mm, while the web has a thickness of 5 mm. Note that the global y direction corresponds to the local negative z direction, and the global z direction corresponds to the local y direction. In the following, uppercase subscripts are used for the global directions and lowercase subscripts for the local directions.
Figure 2: The beam cross section with local direction indicated.
For a detailed analysis, a case where the corners between the flange and the web are rounded are also studied. A 4 mm radius fillet is used at the external corner and a 2 mm radius fillet at the internal corner. This geometry is considered using the Beam Cross Section interface.
GEOMETRY
•
Beam length, L = 1 m
•
Cross-section area A = 4.90·10-4 m2 (from the cross section library)
•
Area moment of inertia in stiff direction, Izz = 1.69·10-7 m4
•
Area moment of inertia in weak direction, Iyy = 2.77·10-8 m4
•
Torsional constant, J = 5.18 ·10-9 m4
•
Position of the shear center (SC) with respect to the area center of gravity (CG), ez = 0.0148 m
•
Torsional section modulus Wt = 8.64·10-7 m3
•
Ratio between maximum and average shear stress for shear in y direction, μy=2.44
•
Ratio between maximum and average shear stress for shear in z direction, μz=2.38
•
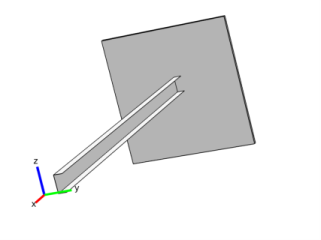
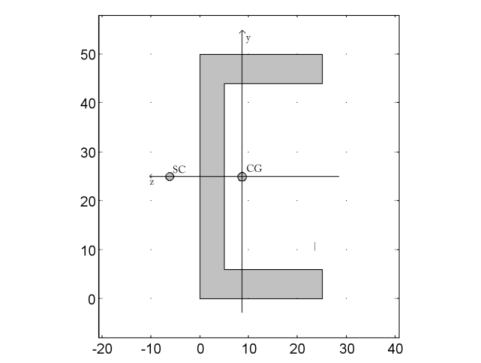
Locations for axial stress evaluation are positioned at the outermost corners of the profile at the points
(y1, z1)=(−0.025, −0.0164)
(y2, z2)=(0.025, −0.0164)
(y3, z3)=(0.025, 0.0086),
(y4, z4)=(−0.025, 0.0086)
measured in the local coordinate system. The indices of the coordinates are point identifiers.
The values above are based on the idealized geometry with sharp corners. In a separate study you compute the section properties including fillets, using the Beam Cross Section interface.
Material
•
Young’s modulus, E = 210 GPa
•
Poisson’s ratio, ν = 0.25
•
Mass density, ρ = 7800 kg/m3
Constraints
One end of the beam is fixed.
Loads
In the first load case, the beam is subjected to three forces and one twisting moment at the tip. The values are:
•
Axial force FX = 10 kN
•
Transverse forces FY = 50 N and FZ = 100 N
•
Twisting moment MX = −10 Nm
In the second load case, the beam is subjected to a gravity load in the negative Z direction.
The third case is an eigenfrequency analysis.
Results and Discussion
The analytical solutions for a slender cantilever beam with loads at the tip are summarized below. The displacements are
The stresses from the axial force, shear force, and torsion are constant along the beam, while the bending moment and bending stresses, are largest at the fixed end. The axial stresses at the fixed end caused by the different loads are computed as
(1)
(2)
In Table 1 the stresses in the stress evaluation points are summarized after insertion of the local coordinates y and z in Equation 1 and Equation 2.
Table 1: Axial stresses in MPA at evaluation points.
Point
Stress from Fx (=FX)
Stress from Fy (=-FZ)
Stress from Fz (=FY)
Total bending stress
Total axial stress
1
20.4
14.8
-29.7
-14.9
5.5
2
20.4
-14.8
-29.7
-44.5
-24.1
3
20.4
-14.8
15.6
0.8
21.2
4
20.4
14.8
15.6
30.4
50.8
Due to the shear forces and twisting moment there are also shear stresses in the section. In general, the shear stresses have a complex distribution, which depends strongly on the geometry of the actual cross section. The peak values of the shear stress contributions from shear forces are
The peak value of the shear stress created by torsion is
Since the general cross-section data used for the analysis cannot predict the exact locations of the peak stresses from each type of action, a conservative scheme for combining the stresses is used in COMSOL Multiphysics. If the computed results exceeds allowable values somewhere in a beam structure, this may be due to this conservatism. You must then check the details, using information about the exact type of cross section and combination of loadings. This can be done using the Beam Cross Section interface.
The conservative maximum shear stresses are created by adding the maximum shear stress from torsion to the maximum shear stresses from shear force:
A conservative equivalent stress is then computed as
The maximum normal stress, σmax, is taken as the highest absolute value in the any of the stress evaluation points (the rightmost column in Table 1).
The COMSOL results for the first load case give 58.6 MPa von Mises stress at the constrained end of the beam which is in total agreement with the analytical solution. Actually, the results would have been the same with any mesh density, because the formulation of the beam elements in COMSOL contains the exact solutions to beam problems with only point loads.
In the second load case there is an evenly distributed gravity load. Since the resultant of a gravity load acts through the mass center of the beam, it does not just cause pure bending but also a twist of the beam. The reason is that in order to cause pure bending, a transverse force must act through the shear center of the section. In COMSOL Multiphysics this effect is automatically accounted for when you apply an edge load. An additional edge moment is created, using the ez (or, depending on load direction, ey) cross section property. The analytical solution to the tip deflections in the self-weight problem is
Also for this case, the COMSOL Multiphysics solution captures the analytical solution exactly. Note, however, that in this case the resolution of the stresses is mesh dependent.
When using a shear center offset as in this example, you must bear in mind that the beam theory assumes that torsional moments and shear forces are applied at the shear center, while axial forces and bending moments are referred to the center of gravity. Thus, when point loads are applied it may be necessary to account for this offset.
The mode shapes and the natural frequencies of the beam are of three types: tension, torsion, and bending. The analytical expressions for the natural frequencies of the different types are:
(3)
(4)
(5)
In Table 2 the computed results are compared with the results from Equation 3, Equation 4, and Equation 5. The agreement is generally very good. The largest difference occurs in Mode 12. This is the fifth order torsional mode, for which the mesh is not sufficient for a high accuracy resolution.
Table 2: Comparison between analytical and computed natural frequencies.
Mode number
Mode type
Analytical frequency (Hz)
COMSOL result (Hz)
1
First y bending
21.02
21.04
2
First z bending
51.96
51.96
3
First torsion
128.3
128.4
4
Second y bending
131.7
131.8
5
Second z bending
325.5
325.7
6
Third y bending
368.8
369.2
7
Second torsion
384.9
388.4
8
Third torsion
641.5
658.1
9
Fourth y bending
722.8
724.1
10
Fourth torsion
898.1
943.7
11
Third z bending
911.8
912.0
12
Fifth torsion
1155
1251
13
Fifth y bending
1196
1199
14
First axial
1250
1251
When the computed section forces at the constrained end of the beam are fed into the Beam Cross Section interface, Figure 3 below shows the von Mises stress distribution within the cross section. One can notice that the maximum stress value is about 66 MPa which is slightly higher than the value computed in the beam interface (58 MPa). The stress computed with analytical cross section data is slightly underestimated. The reason is that the geometric representation used includes the fillets. If exactly the same cross section data are used, the stresses computed by the Beam interface are always conservative.
In Figure 4 to Figure 6 examples are shown of how the stress distributions from the individual section forces are displayed in the Beam Cross Section interface.
Figure 3: von Mises stress distribution at the fixed end (x = 0).
Figure 4: Plot of stresses from a bending moment. The center of gravity is highlighted.
Figure 5: Plot of stresses from shear force. The shear center is highlighted.
Figure 6: Plot of shear stresses from torsion.
Table 3 lists the beam cross section data computed using the Beam Cross Section interface and a geometry with fillets. There are significant differences in the maximum shear stress factor and torsional section modulus values. The stress concentration around the round corner explains these differences.
Table 3: Computed beam cross section data.
Parameter
Value
Area
4.8485e-4 m2
First moment of inertia
1.6556e-7 m4
Distance to shear center in the first principal direction
0.014611 m
Second moment of inertia
2.7252e-8 m4
Distance to shear center in the second principal direction
-9.5565e-9 m
Torsional constant
4.79754e-9 m4
Torsional section modulus
5.6922e-7 m3
Max shear stress factor in the second principal direction
3.0504
Max shear stress factor in the first principal direction
3.6711
If these cross section data are used in the Beam interface, the maximum von Mises stress is 73 MPa, which is slightly above the real value.
Application Library path: Structural_Mechanics_Module/Verification_Examples/channel_beam
Modeling Instructions
From the File menu, choose New.
New
In the New window, click  Model Wizard.
Model Wizard
1
In the Model Wizard window, click  3D.
2
In the Select Physics tree, select Structural Mechanics>Beam (beam).
3
Click Add.
4
Click  Study.
5
In the Select Study tree, select General Studies>Stationary.
6
Click  Done.
Global Definitions
Parameters 1
1
In the Model Builder window, under Global Definitions click Parameters 1.
2
In the Settings window for Parameters, locate the Parameters section.
3
In the table, enter the following settings:
Name
Expression
Value
Description
h1
25[mm]
0.025 m
Flange width
h2
50[mm]
0.05 m
Section height
t1
5[mm]
0.005 m
Web thickness
t2
6[mm]
0.006 m
Flange thickness
L
1[m]
1 m
Beam length
Eb
2e11[Pa]
2E11 Pa
Young's modulus
nub
0.25
0.25
Poisson's ratio
rhob
8000[kg/m^3]
8000 kg/m³
Density
FX
10e3[N]
10000 N
Force in X direction
FY
50[N]
50 N
Force in Y direction
FZ
100[N]
100 N
Force in Z direction
MX
-10[N*m]
-10 N·m
Moment in X direction
Load Group 1
1
In the Model Builder window, right-click Global Definitions and choose Load and Constraint Groups>Load Group.
2
In the Settings window for Load Group, type edge in the Parameter name text field.
Load Group 2
1
In the Model Builder window, right-click Load and Constraint Groups and choose Load Group.
2
In the Settings window for Load Group, type point in the Parameter name text field.
Geometry 1
Polygon 1 (pol1)
1
In the Geometry toolbar, click  More Primitives and choose Polygon.
2
In the Settings window for Polygon, locate the Coordinates section.
3
In the table, enter the following settings:
x (m)
y (m)
z (m)
0
0
0
1
0
0
4
Click  Build All Objects.
Materials
Material 1 (mat1)
1
In the Model Builder window, under Component 1 (comp1) right-click Materials and choose Blank Material.
2
In the Settings window for Material, locate the Material Contents section.
3
In the table, enter the following settings:
Property
Variable
Value
Unit
Property group
Young’s modulus
E
Eb
Pa
Basic
Poisson’s ratio
nu
nub
1
Basic
Density
rho
rhob
kg/m³
Basic
Definitions
Define the cross section parameters to compute the analytical values of the displacement and section forces of the beam.
Variables 1
1
In the Model Builder window, under Component 1 (comp1) right-click Definitions and choose Variables.
2
In the Settings window for Variables, locate the Variables section.
3
In the table, enter the following settings:
Name
Expression
Unit
Description
Gb
Eb/(2*(1+nub))
Pa
Shear Modulus
A
4.9e-4[m^2]
m²
Cross section area
Iyy
2.77e-8[m^4]
m^4
Area moment of inertia, y component
Izz
1.69e-7[m^4]
m^4
Area moment of inertia, z component
Jbeam
5.18e-9[m^4]
m^4
Torsion constant
Wt
8.64e-7[m^3]
m³
Torsion section modulus
ey
0[m]
m
Shear center relative to centroid, y-coordinate
ez
0.0148[m]
m
Shear center relative to centroid, z-coordinate
muy
2.44
 
Max shear stress factor in local y direction
muz
2.38
 
Maximum shear stress factor in local z direction
y1
-0.025[m]
m
Evaluation point 1, local y-coordinate
z1
-0.0164[m]
m
Evaluation point 1, local z-coordinate
y2
0.025[m]
m
Evaluation point 2, local y-coordinate
z2
-0.0164[m]
m
Evaluation point 2, local z-coordinate
y3
0.025[m]
m
Evaluation point 3, local y-coordinate
z3
0.0086[m]
m
Evaluation point 3, local z-coordinate
y4
-0.025[m]
m
Evaluation point 4, local y-coordinate
z4
0.0086[m]
m
Evaluation point 4, local z-coordinate
Define an analytic function to evaluate the bending stress at different locations of the cross section.
sigmabx
1
In the Home toolbar, click  Functions and choose Global>Analytic.
2
In the Settings window for Analytic, type sigmabx in the Function name text field.
3
Locate the Definition section. In the Expression text field, type -FZ*L*y/comp1.Izz+FY*L*z/comp1.Iyy.
4
In the Arguments text field, type y, z.
5
Locate the Plot Parameters section. In the table, enter the following settings:
Argument
Lower limit
Upper limit
y
-h2/2
h2/2
z
-h1/2
h1/2
6
Locate the Units section. In the Arguments text field, type m, m.
7
In the Function text field, type N/m^2.
8
Right-click Analytic 1 (an1) and choose Rename.
9
In the Rename Analytic dialog box, type sigmabx in the New label text field.
10
Click OK.
Define the variables for analytical values of the displacements, rotations and stresses.
Variables 2
1
In the Model Builder window, right-click Definitions and choose Variables.
2
In the Settings window for Variables, locate the Variables section.
3
In the table, enter the following settings:
Name
Expression
Unit
Description
deltaX
FX*L/(Eb*A)
m
X displacement
deltaY
FY*L^3/(3*Eb*Iyy)
m
Y displacement
deltaZ
FZ*L^3/(3*Eb*Izz)
m
Z displacement
thetaX
MX*L/(Gb*Jbeam)
 
Twist
sigmax_Fx
FX/A
N/m²
Stress due to axial load
tausy_max
muy*FZ/A
N/m²
Maximum shear stress due y force
tausz_max
-muz*FY/A
N/m²
Maximum shear stress due to z force
taut_max
abs(MX)/Wt
N/m²
Shear stress due to torsion
tauxz_max
abs(tausz_max)+taut_max
N/m²
Maximum shear stress, z component
tauxy_max
abs(tausy_max)+taut_max
N/m²
Maximum shear stress, y component
sigx1
sigmax_Fx+sigmabx(y1,z1)
N/m²
Normal stress at point 1
sigx2
sigmax_Fx+sigmabx(y2,z2)
N/m²
Normal stress at point 2
sigx3
sigmax_Fx+sigmabx(y3,z3)
N/m²
Normal stress at point 3
sigx4
sigmax_Fx+sigmabx(y4,z4)
N/m²
Normal stress at point 4
sigx_max
max(max(max(sigx1,sigx2),sigx3),sigx4)
N/m²
Maximum normal stress in cross section
sig_mises
sqrt(sigx_max^2+3*tauxy_max^2+3*tauxz_max^2)
N/m²
Maximum von Mises stress
deltaZ_g
-rhob*g_const*A*L^4/(8*Eb*Izz)
m
Z displacement due to gravity load
thetaX_g
rhob*g_const*A*ez*L^2/(2*Gb*Jbeam)
 
Twist due to gravity load
Beam (beam)
Cross-Section Data 1
1
In the Model Builder window, under Component 1 (comp1)>Beam (beam) click Cross-Section Data 1.
2
In the Settings window for Cross-Section Data, locate the Cross-Section Definition section.
3
From the list, choose Common sections.
4
From the Section type list, choose U-profile.
5
In the hy text field, type h2.
6
In the hz text field, type h1.
7
In the ty text field, type t2.
8
In the tz text field, type t1.
Section Orientation 1
1
In the Model Builder window, click Section Orientation 1.
2
In the Settings window for Section Orientation, locate the Section Orientation section.
3
From the Orientation method list, choose Orientation vector.
4
Specify the V vector as
0
X
0
Y
1
Z
Gravity 1
1
In the Physics toolbar, click  Edges and choose Gravity.
2
Select Edge 1 only.
3
In the Physics toolbar, click  Load Group and choose Load Group 1.
Fixed Constraint 1
1
In the Physics toolbar, click  Points and choose Fixed Constraint.
2
Select Point 1 only.
Point Load 1
1
In the Physics toolbar, click  Points and choose Point Load.
2
Select Point 2 only.
3
In the Settings window for Point Load, locate the Force section.
4
Specify the FP vector as
FX
x
FY
y
FZ
z
5
Locate the Moment section. Specify the MP vector as
MX
x
0
y
0
z
6
In the Physics toolbar, click  Load Group and choose Load Group 2.
Study 1
Step 1: Stationary
1
In the Model Builder window, under Study 1 click Step 1: Stationary.
2
In the Settings window for Stationary, click to expand the Study Extensions section.
3
Select the Define load cases check box.
4
Click  Add twice to add two rows to the load case table.
5
In the table, enter the following settings:
Load case
edge
Weight
point
Weight
Point load
 
1.0
√
1.0
Edge load
√
1.0
 
1.0
6
In the Model Builder window, right-click Study 1 and choose Rename.
7
In the Rename Study dialog box, type Stationary Study: Beam in the New label text field.
8
Click OK.
9
In the Home toolbar, click  Compute.
Results
Stress (beam)
The first default plot shows the von Mises stress distribution for the second load case. You can switch to the first load case to evaluate von Mises stress distribution caused by the point load.
1
In the Settings window for 3D Plot Group, locate the Data section.
2
From the Load case list, choose Point load.
3
In the Stress (beam) toolbar, click  Plot.
The following steps illustrate how to evaluate the displacement and stress values in specific tables.
Case1: Displacement/Rotation
1
In the Results toolbar, click  Point Evaluation.
2
In the Settings window for Point Evaluation, type Case1: Displacement/Rotation in the Label text field.
3
Locate the Data section. From the Parameter selection (Load case) list, choose First.
4
Select Point 2 only.
5
Click Replace Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Beam>Displacement>Displacement field - m>u - Displacement field, x component.
6
Click Add Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Definitions>Variables>deltaX - X displacement - m.
7
Click Add Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Beam>Displacement>Displacement field - m>v - Displacement field, y component.
8
Click Add Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Definitions>Variables>deltaY - Y displacement - m.
9
Click Add Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Beam>Displacement>Displacement field - m>w - Displacement field, z component.
10
Click Add Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Definitions>Variables>deltaZ - Z displacement - m.
11
Click Add Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Beam>Displacement>Rotation field - rad>thx - Rotation field, X component.
12
Click Add Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Definitions>Variables>thetaX - Twist.
13
Locate the Expressions section. In the table, enter the following settings:
Expression
Unit
Description
u
m
delta_x computed
deltaX
m
delta_x analytical
v
m
delta_y computed
deltaY
m
delta_y analytical
w
m
delta_z computed
deltaZ
m
delta_z analytical
thx
rad
theta_x computed
thetaX
1
theta_x analytical
14
Click  Evaluate.
Case1: Displacement/Rotation
1
In the Model Builder window, expand the Results>Tables node, then click Table 1.
2
In the Settings window for Table, type Case1: Displacement/Rotation in the Label text field.
Case2: Displacement/Rotation
1
In the Results toolbar, click  Point Evaluation.
2
In the Settings window for Point Evaluation, type Case2: Displacement/Rotation in the Label text field.
3
Select Point 2 only.
4
Locate the Data section. From the Parameter selection (Load case) list, choose Last.
5
Click Replace Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Beam>Displacement>Displacement field - m>w - Displacement field, z component.
6
Click Add Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Definitions>Variables>deltaZ_g - Z displacement due to gravity load - m.
7
Click Add Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Beam>Displacement>Rotation field - rad>thx - Rotation field, X component.
8
Click Add Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Definitions>Variables>thetaX_g - Twist due to gravity load.
9
Locate the Expressions section. In the table, enter the following settings:
Expression
Unit
Description
w
m
delta_z computed
deltaZ_g
m
delta_z analytical
thx
rad
theta_x computed
thetaX_g
1
theta_x analytical
10
Click  Evaluate.
Case2: Displacement/Rotation
1
In the Model Builder window, under Results>Tables click Table 2.
2
In the Settings window for Table, type Case2: Displacement/Rotation in the Label text field.
Axial Stress from Fx
1
In the Results toolbar, click  Point Evaluation.
2
Select Point 2 only.
3
In the Settings window for Point Evaluation, locate the Data section.
4
From the Parameter selection (Load case) list, choose First.
5
In the Label text field, type Axial Stress from Fx.
6
Click Replace Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Beam>Stress>Stress variables at first evaluation point>beam.s1 - Normal stress at first evaluation point - N/m².
7
Click Add Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Beam>Stress>Stress variables at second evaluation point>beam.s2 - Normal stress at second evaluation point - N/m².
8
Click Add Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Beam>Stress>Stress variables at third evaluation point>beam.s3 - Normal stress at third evaluation point - N/m².
9
Click Add Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Beam>Stress>Stress variables at fourth evaluation point>beam.s4 - Normal stress at fourth evaluation point - N/m².
10
Locate the Expressions section. In the table, enter the following settings:
Expression
Unit
Description
beam.s1
MPa
first point
beam.s2
MPa
second point
beam.s3
MPa
third point
beam.s4
MPa
fourth point
11
Click  Evaluate.
Normal Stress from Fx
1
In the Model Builder window, under Results>Tables click Table 3.
2
In the Settings window for Table, type Normal Stress from Fx in the Label text field.
Total Bending Stress
1
In the Results toolbar, click  Point Evaluation.
2
In the Settings window for Point Evaluation, type Total Bending Stress in the Label text field.
3
Locate the Data section. From the Parameter selection (Load case) list, choose First.
4
Select Point 1 only.
5
Click Replace Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Beam>Stress>Stress variables at first evaluation point>beam.sb1 - Bending stress at first evaluation point - N/m².
6
Click Add Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Definitions>Functions>sigmabx(y, z) - sigmabx.
7
Click Add Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Beam>Stress>Stress variables at second evaluation point>beam.sb2 - Bending stress at second evaluation point - N/m².
8
Click Add Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Definitions>Functions>sigmabx(y, z) - sigmabx.
9
Click Add Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Beam>Stress>Stress variables at third evaluation point>beam.sb3 - Bending stress at third evaluation point - N/m².
10
Click Add Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Definitions>Functions>sigmabx(y, z) - sigmabx.
11
Click Add Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Beam>Stress>Stress variables at fourth evaluation point>beam.sb4 - Bending stress at fourth evaluation point - N/m².
12
Click Add Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Definitions>Functions>sigmabx(y, z) - sigmabx.
13
Locate the Expressions section. In the table, enter the following settings:
Expression
Unit
Description
beam.sb1
MPa
first point, computed
sigmabx(y1, z1)
MPa
first point, analytical
beam.sb2
MPa
second point, computed
sigmabx(y2, z2)
MPa
second point, analytical
beam.sb3
MPa
third point, computed
sigmabx(y3, z3)
MPa
third point, analytical
beam.sb4
MPa
fourth point, computed
sigmabx(y4, z4)
MPa
fourth point, analytical
14
Click  Evaluate.
Total Bending Stress
1
In the Model Builder window, under Results>Tables click Table 4.
2
In the Settings window for Table, type Total Bending Stress in the Label text field.
Shear Stress
1
In the Results toolbar, click  Point Evaluation.
2
In the Settings window for Point Evaluation, type Shear Stress in the Label text field.
3
Locate the Data section. From the Parameter selection (Load case) list, choose First.
4
Select Point 1 only.
5
Click Replace Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Beam>Stress>beam.tsymax - Max shear stress from shear force, y direction - N/m².
6
Click Add Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Definitions>Variables>tausy_max - Maximum shear stress due y force - N/m².
7
Click Add Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Beam>Stress>beam.tszmax - Max shear stress from shear force, z direction - N/m².
8
Click Add Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Definitions>Variables>tausz_max - Maximum shear stress due to z force - N/m².
9
Click Add Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Beam>Stress>beam.ttmax - Max torsional shear stress - N/m².
10
Click Add Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Definitions>Variables>taut_max - Shear stress due to torsion - N/m².
11
Click Add Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Beam>Stress>beam.txymax - Max shear stress, y direction - N/m².
12
Click Add Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Definitions>Variables>tauxy_max - Maximum shear stress, y component - N/m².
13
Click Add Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Beam>Stress>beam.txzmax - Max shear stress, z direction - N/m².
14
Click Add Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Definitions>Variables>tauxz_max - Maximum shear stress, z component - N/m².
15
Locate the Expressions section. In the table, enter the following settings:
Expression
Unit
Description
beam.tsymax
MPa
Max shear stress from shear force, y direction (Computed)
tausy_max
MPa
Max shear stress from shear force, y direction (Analytical)
beam.tszmax
MPa
Max shear stress from shear force, z direction (Computed)
tausz_max
MPa
Max shear stress from shear force, z direction (Analytical)
beam.ttmax
MPa
Max torsional shear stress (Computed)
taut_max
MPa
Max torsional shear stress (Analytical)
beam.txymax
MPa
Max shear stress, y direction (Computed)
tauxy_max
MPa
Max shear stress, y direction (Analytical)
beam.txzmax
MPa
Max shear stress, z direction (Computed)
tauxz_max
MPa
Max shear stress, z direction (Analytical)
16
Click  Evaluate.
Perform an eigenfrequency analysis.
Shear Stress
1
In the Model Builder window, under Results>Tables click Table 5.
2
In the Settings window for Table, type Shear Stress in the Label text field.
Add Study
1
In the Home toolbar, click  Add Study to open the Add Study window.
2
Go to the Add Study window.
3
Find the Studies subsection. In the Select Study tree, select General Studies>Eigenfrequency.
4
Click Add Study in the window toolbar.
5
In the Home toolbar, click  Add Study to close the Add Study window.
Eigenfrequency Study: Beam
1
In the Model Builder window, right-click Study 2 and choose Rename.
2
In the Rename Study dialog box, type Eigenfrequency Study: Beam in the New label text field.
3
Click OK.
Step 1: Eigenfrequency
Before computing the study, increase the desired number of eigenfrequencies.
1
In the Model Builder window, under Eigenfrequency Study: Beam click Step 1: Eigenfrequency.
2
In the Settings window for Eigenfrequency, locate the Study Settings section.
3
Select the Desired number of eigenfrequencies check box.
4
In the associated text field, type 20.
5
In the Home toolbar, click  Compute.
Results
Mode Shape (beam)
1
In the Settings window for 3D Plot Group, locate the Data section.
2
From the Eigenfrequency (Hz) list, choose 51.956.
3
In the Mode Shape (beam) toolbar, click  Plot.
The following steps illustrate how to use the Beam Cross Section interface to compute beam physical properties and evaluate stresses within a cross section.
Cut Point 3D 1
Start by evaluating the section forces at the fixed end of the beam. These values are needed to get an accurate stress distribution within the beam cross section. To make it possible to change this location we start by creating a Cut Point.
1
In the Results toolbar, click  Cut Point 3D.
2
In the Settings window for Cut Point 3D, locate the Point Data section.
3
In the X text field, type 0.
4
In the Y text field, type 0.
5
In the Z text field, type 0.
Section Forces
1
In the Results toolbar, click  Point Evaluation.
2
In the Settings window for Point Evaluation, type Section Forces in the Label text field.
3
Locate the Data section. From the Dataset list, choose Cut Point 3D 1.
4
Locate the Expressions section. In the table, enter the following settings:
Expression
Unit
Description
beam.Nxl
N
N
beam.Mzl
N*m
M1
beam.Tyl
N
T2
beam.Myl
N*m
M2
beam.Tzl
N
T1
beam.Mxl
N*m
Mt
5
Click  Evaluate.
Section Forces
1
In the Model Builder window, under Results>Tables click Table 6.
2
In the Settings window for Table, type Section Forces in the Label text field.
Add Component
In the Model Builder window, right-click the root node and choose Add Component>2D.
Add Physics
1
In the Home toolbar, click  Add Physics to open the Add Physics window.
2
Go to the Add Physics window.
3
In the tree, select Structural Mechanics>Beam Cross Section (bcs).
4
Find the Physics interfaces in study subsection. In the table, clear the Solve check boxes for Stationary Study: Beam and Eigenfrequency Study: Beam.
5
Click Add to Component 2 in the window toolbar.
6
In the Home toolbar, click  Add Physics to close the Add Physics window.
Add Study
1
In the Home toolbar, click  Add Study to open the Add Study window.
2
Go to the Add Study window.
3
Find the Studies subsection. In the Select Study tree, select General Studies>Stationary.
4
Find the Physics interfaces in study subsection. In the table, clear the Solve check box for Beam (beam).
5
Click Add Study in the window toolbar.
6
In the Model Builder window, click the root node.
7
In the Home toolbar, click  Add Study to close the Add Study window.
Component 2 (comp2)
In the Model Builder window, collapse the Component 2 (comp2) node.
Stationary Study: Beam Cross Section
1
In the Model Builder window, right-click Study 3 and choose Rename.
2
In the Rename Study dialog box, type Stationary Study: Beam Cross Section in the New label text field.
3
Click OK.
Use the predefined Generic C-beam geometry part to draw the beam section geometry.
Geometry 2
In the Model Builder window, under Component 2 (comp2) click Geometry 2.
Part Libraries
1
In the Home toolbar, click  Windows and choose Part Libraries.
2
In the Part Libraries window, select Structural Mechanics Module>Beams>Generic>C_beam_generic in the tree.
3
Click  Add to Geometry.
Geometry 2
Generic C-beam 1 (pi1)
1
In the Model Builder window, under Component 2 (comp2)>Geometry 2 click Generic C-beam 1 (pi1).
2
In the Settings window for Part Instance, locate the Input Parameters section.
3
In the table, enter the following settings:
Name
Expression
Value
Description
d
h2
0.05 m
Beam height
b
h1
0.025 m
Flange width
tw
t1
0.005 m
Web thickness
tf
t2
0.006 m
Flange thickness
r1
2[mm]
0.002 m
Web fillet radius
r2
0
0 mm
Flange fillet radius
slope
0
0
Flange slope [%]
u
0
0 mm
Flange thickness evaluation location
Form Union (fin)
1
In the Model Builder window, click Form Union (fin).
2
In the Settings window for Form Union/Assembly, click  Build Selected.
3
Click the  Zoom Extents button in the Graphics toolbar.
Beam Cross Section (bcs)
Input the section force data evaluated previously from the Beam into Beam Cross Section. To automate this process of transferring the section forces at any arbitrary location, create a model method first.
New Method
1
In the Developer toolbar, click  New Method.
2
In the New Method dialog box, type EvaluateSectionForces in the Name text field.
3
Click OK.
Application Builder
EvaluateSectionForces
1
In the Application Builder window, under Methods click EvaluateSectionForces.
2
Copy the following code into the EvaluateSectionForces window:
double Len = model.param().evaluate("L");
String xPos = xp;
try {
double xP = Double.valueOf(xp);
if (xP < 0) {
alert("Evaluation point out of range. Using the root of the beam for evaluation.", "Evaluation point out of range warning");
xPos = "0"
}
if (xP > Len) {
alert("Evaluation point out of range. Using the tip of the beam for evaluation.", "Evaluation point out of range warning");
xPos = "L";
}
} catch (Exception e) {

}

with(model.result().dataset("cpt1"));
set("pointx", xPos);
endwith();

double[][] SecForce = model.result().numerical("pev6").getReal();
with(model.component("comp2").physics("bcs").prop("UserInput"));
set("N", Double.toString(SecForce[0][0]));
set("M1", Double.toString(SecForce[1][0]));
set("T2", Double.toString(SecForce[2][0]));
set("M2", Double.toString(SecForce[3][0]));
set("T1", Double.toString(SecForce[4][0]));
set("Mt", Double.toString(SecForce[5][0]));
endwith();
3
In the Settings window for Method, locate the Inputs and Output section.
4
Find the Inputs subsection. Click  Add.
5
In the table, enter the following settings:
Name
Type
Default
Description
Unit
xp
String
0
 
 
Methods
In the Home toolbar, click  Model Builder to switch to the main desktop.
Global Definitions
Click  Method Call and choose EvaluateSectionForces.
EvaluateSectionForces 1
Run the method EvaluateSectionForces to transfer the cross section forces in Beam Cross Section interface.
1
Click  Run Method Call and choose EvaluateSectionForces 1.
Stationary Study: Beam Cross Section
Click  Compute.
Results
Bending Moment M1 (bcs)
Evaluate the beam physical properties required for the Beam interface.
Section Properties
In the Model Builder window, right-click Section Properties and choose Evaluate>New Table.
Section Properties
1
In the Model Builder window, under Results>Tables click Table 7.
2
In the Settings window for Table, type Section Properties in the Label text field.
Beam (beam)
In the Model Builder window, under Component 1 (comp1) click Beam (beam).
Cross-Section Data 2
1
In the Physics toolbar, click  Edges and choose Cross-Section Data.
2
Select Edge 1 only.
3
In the Settings window for Cross-Section Data, locate the Basic Section Properties section.
4
In the A text field, type comp2.bcs.A.
5
In the Izz text field, type comp2.bcs.I1.
6
In the ez text field, type comp2.bcs.ei1.
7
In the Iyy text field, type comp2.bcs.I2.
8
In the ey text field, type comp2.bcs.ei2.
9
In the J text field, type comp2.bcs.J.
10
Click to expand the Stress Evaluation Properties section. In the hy text field, type comp2.bcs.h2.
11
In the hz text field, type comp2.bcs.h1.
12
In the wt text field, type comp2.bcs.Wt.
13
In the μy text field, type comp2.bcs.mu2.
14
In the μz text field, type comp2.bcs.mu1.
Section Orientation 1
1
In the Model Builder window, expand the Cross-Section Data 2 node, then click Section Orientation 1.
2
In the Settings window for Section Orientation, locate the Section Orientation section.
3
Specify the P vector as
0
X
0
Y
1
Z
Add Study
1
In the Home toolbar, click  Add Study to open the Add Study window.
2
Go to the Add Study window.
3
Find the Studies subsection. In the Select Study tree, select General Studies>Stationary.
4
Find the Physics interfaces in study subsection. In the table, clear the Solve check box for Beam Cross Section (bcs).
5
Click Add Study in the window toolbar.
6
In the Home toolbar, click  Add Study to close the Add Study window.
Stationary Study: Beam (Inputs from Beam Cross Section)
1
In the Model Builder window, click Study 4.
2
In the Settings window for Study, locate the Study Settings section.
3
Clear the Generate default plots check box.
4
Right-click Study 4 and choose Rename.
5
In the Rename Study dialog box, type Stationary Study: Beam (Inputs from Beam Cross Section) in the New label text field.
6
Click OK.
Step 1: Stationary
Some cross section properties are now defined using a dependent variable from the Beam Cross Section Interface. An example is the torsional section modulus defined as comp2.bcs.Wt. Follow the steps below to get access to these variables in this study.
1
In the Settings window for Stationary, click to expand the Values of Dependent Variables section.
2
Find the Values of variables not solved for subsection. From the Settings list, choose User controlled.
3
From the Method list, choose Solution.
4
From the Study list, choose Stationary Study: Beam Cross Section, Stationary.
5
Locate the Study Extensions section. Select the Define load cases check box.
6
Click  Add.
7
In the table, enter the following settings:
Load case
edge
Weight
point
Weight
Point Load
 
1.0
√
1.0
8
In the Home toolbar, click  Compute.
Compare the von Mises stress for the two cross sections.
Results
von Mises Stress
1
In the Results toolbar, click  Point Evaluation.
2
In the Settings window for Point Evaluation, type von Mises Stress in the Label text field.
3
Locate the Data section. From the Parameter selection (Load case) list, choose First.
4
Select Point 1 only.
5
Click Replace Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Beam>Stress>beam.mises - von Mises stress - N/m².
6
Locate the Expressions section. In the table, enter the following settings:
Expression
Unit
Description
beam.mises
MPa
von Mises stress
7
Click  Evaluate.
8
Locate the Data section. From the Dataset list, choose Stationary Study: Beam (Inputs from Beam Cross Section)/Solution 4 (5) (sol4).
9
Click  Evaluate.
von Mises Stress
1
In the Model Builder window, under Results>Tables click Table 8.
2
In the Settings window for Table, type von Mises Stress in the Label text field.
Finally modify Study 1 and Study 2 so that you can re-compute the solution later.
Stationary Study: Beam
Step 1: Stationary
1
In the Model Builder window, under Stationary Study: Beam click Step 1: Stationary.
2
In the Settings window for Stationary, locate the Physics and Variables Selection section.
3
Select the Modify model configuration for study step check box.
4
In the Physics and variables selection tree, select Component 1 (comp1)>Beam (beam)>Cross-Section Data 2.
5
Click  Disable.
Eigenfrequency Study: Beam
Step 1: Eigenfrequency
1
In the Model Builder window, under Eigenfrequency Study: Beam click Step 1: Eigenfrequency.
2
In the Settings window for Eigenfrequency, locate the Physics and Variables Selection section.
3
Select the Modify model configuration for study step check box.
4
In the Physics and variables selection tree, select Component 1 (comp1)>Beam (beam)>Cross-Section Data 2.
5
Click  Disable.