Fluid-Structure Interaction in a Network of Blood Vessels

This example studies a portion of the vascular system, in particular the upper part of the aorta (Figure 1). The aorta and its ramified blood vessels are embedded in biological tissue, specifically the cardiac muscle. The flowing blood applies pressure to the artery’s internal surfaces and its branches, thereby deforming the tissue. The analysis consists of two distinct but coupled procedures: first, a fluid-dynamics analysis including a calculation of the velocity field and pressure distribution in the blood (variable in time and in space); second, a mechanical analysis of the deformation of the tissue and artery. Any change in the shape of the vessel walls does not influence the fluid domain, which implies that there is only a unidirectional fluid-structural coupling.

Figure 1: The model domain consists of part of the aorta, its branches, and the surrounding tissue.

Model Definition

Figure 2 shows two views of the model domain, one with and one without the cardiac muscle. The mechanical analysis must consider the cardiac muscle because it presents a stiffness that resists artery deformation due to the applied pressure.

Figure 2: A view of the aorta and its ramification (branching vessels) with blood contained, shown both with (left) and without (right) the cardiac muscle.

The main characteristics of the analyses are:

•

Fluid dynamics analysis

Here the Navier-Stokes equations are solved in the blood domain. At each surface where the model brings a vessel to an abrupt end, it represents the load with a known pressure distribution.

•

Mechanical analysis

Only the domains related to the biological tissues are active in this analysis. The model represents the load with the total stress distribution it computes during the fluid-dynamics analysis.

Analysis of Rubber-like Tissue and Artery Material Models

Generally, the modeling of biological tissue is an advanced subject for several reasons:

•

The material can undergo very large strains (finite deformations).

•

The stress-strain relationship is generally nonlinear.

•

Many hyperelastic materials are almost incompressible. You must then revise standard displacement-based finite element formulations in order to arrive at correct results (mixed formulations).

You must pay particular attention to the definition of stress and strain measures. In a geometrically nonlinear analysis the assumptions about infinitesimal displacements are no longer valid. It is necessary to consider geometrical nonlinearity in a model when:

•

Significant rigid-body rotations occur (finite rotations).

•

The strains are no longer small (larger than a few percent).

•

The loading of the body depends on the deformation.

All of these issues are dealt with in the hyperelastic material model built-in the Nonlinear Structural Materials Module.

In this case, the displacements and strains are so small that it is sufficient to use a linear elastic material model. The material data is given for a neo-Hookean hyperelastic material, but in the small strain limit the interpretation of the material constants is the same for a linear elastic material.

Materials

The following material properties are used:

•

Blood

density = 1060 kg/m3

dynamic viscosity = 0.005 Ns/m2

•

Artery

density = 960 kg/m3

Linear elastic behavior: the Lame’ parameter μ equals 6.20·106 N/m2, while the other Lame’ parameter λ equals 20μ.

•

Cardiac muscle

density = 1200 kg/m3

Linear elastic behavior: the Lame’ parameter μ equals 7.20·106 N/m2, while the other Lame’ parameter λ equals 20μ.

Fluid Dynamics Analysis

The fluid dynamics analysis considers the solution of the 3D Navier-Stokes equations. You can do so in both a stationary case or in the time domain. To establish the boundary conditions, six pressure conditions are applied with the configuration shown in Figure 3.

Figure 3: Boundary conditions for the fluid-flow analysis.

The pressure conditions are:

•

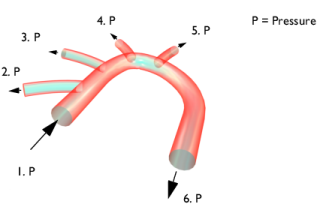
Section 1: 126.09 mmHg

•

Section 2: 125.91 mmHg

•

Section 3: 125.415 mmHg

•

Section 4: 125.415 mmHg

•

Section 5: 125.415 mmHg

•

Section 6: 125.1 mmHg

Those pressure values are the mean values over a heart beating cycle. During a cycle the pressure varies between a minimal and a maximal value which is calculated thanks to a relative amplitude α. For the time-dependent analysis, a simple trigonometric function is used for varying the pressure distribution over time:

The first piece of function between 0 and 0.5 s has no physical significance, it is just a ramp that enables you to calculate the initial state. The second piece of function makes the pressure vary between its minimal and maximal value during a 1 s cycle.

You implement this effect in COMSOL Multiphysics using a Piecewise function.

Results and Discussion

The flow field at the time t=1 s is displayed in Figure 4 as a slice plot.

Figure 4: Velocity field in the aorta and its ramification (branching).

Figure 5 shows the total displacement at the peak load (after 1 s). The displacements are in the order of 4 μm, which suggests that the unidirectional multiphysics coupling is a reasonable approximation.

Figure 5: Displacements in the blood vessel.

Notes About the COMSOL Implementation

In this example, and many other cases, an analysis which is time dependent for one physics can be treated as quasi-static from the structural mechanics point of view. You can handle this by running the structural analysis as a parametric sweep over a number of static load cases, where the time is used as the parameter. This method is used here.

Structural_Mechanics_Module/Fluid-Structure_Interaction/blood_vessel

Modeling Instructions

From the menu, choose .

New

In the window, click

Model Wizard

In the window, click

In the tree, select .

Click .

Click

In the tree, select .

Click

Global Definitions

Parameters 1

In the window, under click .

In the window for , locate the section.

In the table, enter the following settings:


Name	Expression	Value	Description
t	0[s]	0 s	Time continuation parameter
alpha	1/3	0.33333	Relative pressure amplitude during heart's beating

Piecewise 1 (pw1)

In the toolbar, click

and choose .

In the window for , type f in the text field.

Locate the section. In the text field, type t.

Find the subsection. In the table, enter the following settings:


Start	End	Function
0	0.5	(1-alpha)sin(pit)
0.5	1.5	1-alphacos(2pi*(t-0.5))

Locate the section. In the text field, type s.

In the text field, type 1.

Click

Geometry 1

The geometry for this model is available as an MPHBIN-file. Import this file as follows.

Import 1 (imp1)

In the toolbar, click

In the window for , locate the section.

Click .

Browse to the model’s Application Libraries folder and double-click the file blood_vessel.mphbin.

Click .

The length unit in the imported geometry is centimeters, while the default length unit in COMSOL Multiphysics is meters. Therefore, you need to rescale the geometry.

Scale 1 (sca1)

In the toolbar, click

and choose .

In the window for , locate the section.

In the text field, type 0.01.

Select the object only.

Use to automatically fix small issues in the geometry. This will improve meshing and computation.

Remove Details 1 (rmd1)

In the toolbar, click

In the window for , click

Two faces have been collapsed.

Click the

button in the toolbar.

Form Union (fin)

In the window, click .

In the window for , click

Click the

button in the toolbar to see the interior.

Next, define a number of selections as sets of geometric entities to use when setting up the model.

Definitions

Blood

In the toolbar, click

In the window for , type Blood in the text field.

Select Domain 3 only.

Explicit 2-10

Proceed to create nine explicit selections with the following settings:


Label	Geometric entity level	Selection
Artery	Domain	2
Muscle	Domain	1
Inlet	Boundary	38
Outlet 1	Boundary	19
Outlet 2	Boundary	9
Outlet 3	Boundary	41
Outlet 4	Boundary	70
Outlet 5	Boundary	84
Roller boundaries	Boundary	1-6,12,26,27,30,33,64,67,83,85

The roller boundaries are the free boundaries of muscle and artery that are neither in contact with each other nor with blood.

Loaded boundaries

In the toolbar, click

In the window for , type Loaded boundaries in the text field.

Locate the section. From the list, choose .

Select Boundaries 10, 20, 36, 42, and 68 only.

Select the check box. The selection should now contain boundaries 10–11, 16–17, 20–21, 23–24, 36–37, 39–40, 42–43, 45–46, 50–53, 58–59, 61–62, 68–69, 71–72, 77–78, 80–81.

The loaded boundaries are the inner artery boundaries that are in contact with blood.

Artery walls

In the toolbar, click

In the window for , type Artery walls in the text field.

Select Domain 2 only.

Locate the section. From the list, choose .

Select the check box.

Laminar Flow (spf)

In the window, under click .

In the window for , locate the section.

From the list, choose .

Inlet 1

In the toolbar, click

and choose .

In the window for , locate the section.

From the list, choose .

Locate the section. From the list, choose .

Locate the section. In the p0 text field, type 126.09[mmHg]*f(t).

Outlet 1

In the toolbar, click

and choose .

In the window for , locate the section.

From the list, choose .

Locate the section. In the p0 text field, type 125.91[mmHg]*f(t).

Outlet 2-5

Proceed to add four outlet boundary nodes with the following settings:


Boundary Selection	p0
Outlet 2	125.415[mmHg]*f(t)
Outlet 3	125.415[mmHg]*f(t)
Outlet 4	125.415[mmHg]*f(t)
Outlet 2	125.1[mmHg]*f(t)

Solid Mechanics (solid)

In the window, under click .

Select Domains 1 and 2 only.

Linear Elastic Material 1

In the window, under click .

In the window for , locate the section.

From the list, choose .

Roller 1

In the toolbar, click

and choose .

In the window for , locate the section.

From the list, choose .

Multiphysics

Fluid-Structure Interaction 1 (fsi1)

In the window, under click .

In the window for , locate the section.

From the list, choose to ensure a unidirectional coupling, from the fluid to the solid.

Materials

Blood

In the window, under right-click and choose .

In the window for , type Blood in the text field.

Locate the section. From the list, choose .

Locate the section. In the table, enter the following settings:


Property	Variable	Value	Unit	Property group
Density	rho	1060	kg/m³	Basic
Dynamic viscosity	mu	0.005	Pa·s	Basic

Artery

Right-click and choose .

In the window for , type Artery in the text field.

Locate the section. From the list, choose .

Locate the section. In the table, enter the following settings:


Property	Variable	Value	Unit	Property group
Lamé parameter λ	lambLame	20muLame-2muLame/3	N/m²	Lamé parameters
Lamé parameter μ	muLame	6.20e6	N/m²	Lamé parameters
Density	rho	960	kg/m³	Basic

Muscle

Right-click and choose .

In the window for , type Muscle in the text field.

Locate the section. From the list, choose .

Locate the section. In the table, enter the following settings:


Property	Variable	Value	Unit	Property group
Lamé parameter λ	lambLame	20muLame-2muLame/3	N/m²	Lamé parameters
Lamé parameter μ	muLame	7.20e6	N/m²	Lamé parameters
Density	rho	1200	kg/m³	Basic

Mesh 1

In the window, under click .

In the window for , locate the section.

From the list, choose .

Size

Right-click and choose .

In the window for , locate the section.

Click the button.

Locate the section. In the text field, type 0.0003.

Click

Study 1

The structural problem is quasistatic, so you can use the time as a parameter for the parametric solver, together with a stationary solver. Thus the whole study can be divided into two steps. First run the transient study for the fluid-mechanics part of the problem and then use the stationary solver to solve the structural part using the solution from the first transient study.

Step 1: Time Dependent

In the window, under click .

In the window for , locate the section.

In the text field, type range(0,0.05,1.5).

Locate the section. In the table, clear the check box for .

Stationary

In the toolbar, click

and choose .

In the window for , locate the section.

In the table, clear the check box for .

Click to expand the section. Select the check box.

Click

In the table, enter the following settings:


Parameter name	Parameter value list	Parameter unit
t (Time continuation parameter)	range(0,0.05,1.5)	s

Click to expand the section. Find the subsection. From the list, choose .

From the list, choose .

Solution 1 (sol1)

In the toolbar, click

In the window, expand the node, then click .

In the window for , click to expand the section.

From the list, choose . This way the solver computes at least once between each output time step in order to reduce possible interpolation errors in the fluid-load evaluation.

In the toolbar, click