
|
|
The equation system for heterojunctions is highly nonlinear and numerically challenging. In this tutorial we uses the Semiconductor Equilibrium study step to achieve better convergence. See the verification model example heterojunction_1d for more ways to overcome the numerical challenge.
|
|
1
|
|
2
|
|
3
|
Click Add.
|
|
4
|
Click
|
|
5
|
In the Select Study tree, select Preset Studies for Selected Physics Interfaces>Semiconductor Equilibrium.
|
|
6
|
Click
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
1
|
|
2
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
1
|
In the Model Builder window, under Component 1 (comp1)>Materials click GaN (Zinc Blende) - Gallium Nitride 1 (mat2).
|
|
2
|
|
3
|
|
4
|
|
5
|
Click OK.
|
|
6
|
|
8
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
Click OK.
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|
|
1
|
|
2
|
|
4
|
|
1
|
|
2
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
1
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
1
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
In the Physics and variables selection tree, select Component 1 (comp1)>Semiconductor (semi)>p Contact - Current.
|
|
5
|
Click
|
|
6
|
Click to expand the Values of Dependent Variables section. Find the Initial values of variables solved for subsection. From the Settings list, choose User controlled.
|
|
7
|
|
8
|
|
9
|
|
10
|
Click
|
|
12
|
|
1
|
|
2
|
|
3
|
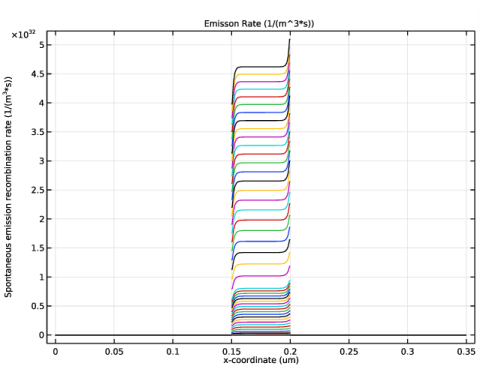
In the associated text field, type x-coordinate (um).
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|
|
1
|
|
2
|
|
3
|
|
4
|
In the associated text field, type x-coordinate (um).
|
|
5
|
|
6
|
|
7
|
|
8
|
|
9
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
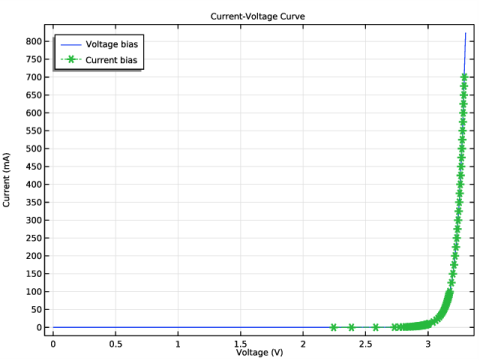
In the associated text field, type Voltage (V).
|
|
8
|
|
9
|
In the associated text field, type Current (mA).
|
|
10
|
|
1
|
|
2
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
Locate the Expressions section. In the table, enter the following settings:
|
|
5
|
Click
|
|
1
|
In the Model Builder window, under Component 1 (comp1)>Semiconductor (semi) click p Contact - Current.
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
Find the Initial values of variables solved for subsection. From the Settings list, choose User controlled.
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|
Click
|
|
10
|
|
1
|
In the Model Builder window, under Results>Current vs. Voltage right-click Global 1 and choose Duplicate.
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
Click to expand the Coloring and Style section. Find the Line style subsection. From the Line list, choose Dashed.
|
|
8
|
|
9
|
|
10
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
In the associated text field, type x-coordinate (um).
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
Locate the Data section. From the Dataset list, choose Current bias study - frequency domain (sol3).
|
|
4
|
|
5
|
|
6
|
|
7
|
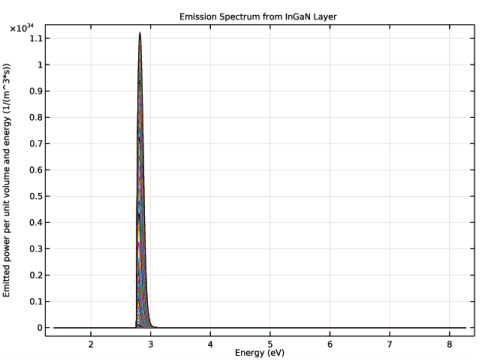
In the associated text field, type Energy (eV).
|
|
8
|
|
9
|
In the associated text field, type Emitted power per unit volume and energy (1/(m^3*s)).
|
|
1
|
|
2
|
|
3
|
|
4
|
Locate the y-Axis Data section. In the Expression text field, type comp1.atxd1(0.1525e-6,semi.ot1.dP_dE).
|
|
5
|
|
6
|
|
7
|
|
1
|
|
2
|
In the Settings window for 1D Plot Group, type Total Emission Rate from InGaN Layer vs. Current in the Label text field.
|
|
3
|
|
4
|
|
5
|
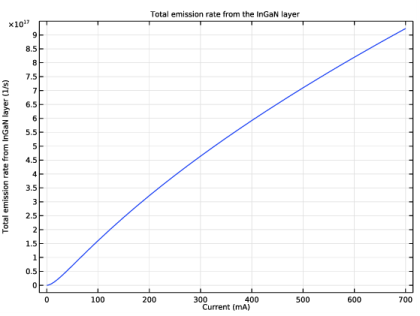
In the associated text field, type Current (mA).
|
|
6
|
|
7
|
In the associated text field, type Total emission rate from InGaN layer (1/s).
|
|
8
|
|
9
|
|
1
|
|
2
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
In the associated text field, type Current Density (A/cm^2).
|
|
6
|
|
7
|
In the associated text field, type Internal Quantum Efficiency.
|
|
8
|
|
9
|
|
1
|
|
2
|
|
4
|
|
5
|
|
6
|
|
7
|