
|
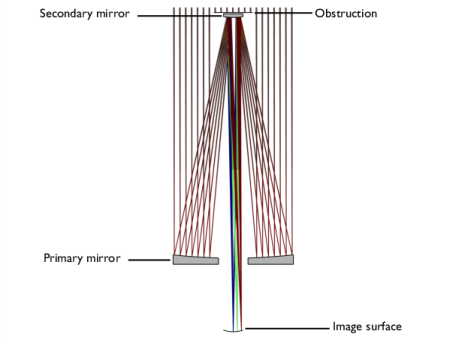
|
1
|
|
2
|
|
3
|
Click Add.
|
|
4
|
Click
|
|
5
|
|
6
|
Click
|
|
1
|
|
2
|
|
3
|
|
4
|
Browse to the model’s Application Libraries folder and double-click the file hubble_space_telescope_parameters.txt.
|
|
1
|
|
2
|
|
3
|
Find the Mesh frame coordinates subsection. From the Geometry shape function list, choose Cubic Lagrange. The ray tracing algorithm used by the Geometrical Optics interface computes the refracted ray direction based on a discretized geometry via the underlying finite element mesh. A cubic geometry shape order usually introduces less discretization error compared to the default, which uses linear and quadratic polynomials.
|
|
1
|
|
2
|
|
3
|
In the Part Libraries window, select Ray Optics Module>3D>Mirrors>conic_mirror_on_axis_3d in the tree.
|
|
4
|
|
5
|
In the Select Part Variant dialog box, select Specify clear aperture diameter in the Select part variant list.
|
|
6
|
Click OK.
|
|
1
|
In the Model Builder window, under Component 1 (comp1)>Geometry 1 click Conic Mirror On Axis 3D 1 (pi1).
|
|
2
|
|
3
|
|
4
|
Locate the Position and Orientation of Output section. Find the Displacement subsection. In the zw text field, type Z_prim.
|
|
5
|
|
6
|
Click to expand the Boundary Selections section. In the table, select the Keep check box for Mirror surface.
|
|
8
|
|
9
|
|
10
|
Click OK.
|
|
11
|
|
1
|
|
2
|
|
3
|
|
4
|
Locate the Position and Orientation of Output section. Find the Coordinate system to match subsection. From the Take work plane from list, choose Primary Mirror (pi1).
|
|
5
|
|
6
|
|
7
|
|
8
|
|
1
|
|
2
|
|
3
|
Locate the Parameters section. Find the First parameter subsection. In the Minimum text field, type -hw_image.
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|
|
9
|
In the z text field, type Cp*(s1^2 + s2^2)/(1 + sqrt(1 - Cp^2*(s1^2 + s2^2)))*1[m]. This is the equation of a sphere having a curvature Cp. This is the Petzval curvature defined in the Parameters node.
|
|
10
|
|
11
|
Locate the Coordinate System section. From the Take work plane from list, choose Secondary Mirror (pi2).
|
|
12
|
|
13
|
Locate the Selections of Resulting Entities section. Select the Resulting objects selection check box.
|
|
1
|
|
2
|
|
3
|
In the Part Libraries window, select Ray Optics Module>3D>Apertures and Obstructions>circular_planar_annulus in the tree.
|
|
4
|
|
1
|
In the Model Builder window, under Component 1 (comp1)>Geometry 1 click Circular Planar Annulus 1 (pi3).
|
|
2
|
|
3
|
|
4
|
Locate the Position and Orientation of Output section. Find the Coordinate system to match subsection. From the Take work plane from list, choose Secondary Mirror (pi2).
|
|
5
|
|
6
|
|
7
|
|
8
|
|
9
|
|
10
|
|
11
|
|
1
|
|
2
|
|
3
|
|
4
|
Locate the Ray Release and Propagation section. In the Maximum number of secondary rays text field, type 0.
|
|
5
|
Select the Use geometry normals for ray-boundary interactions check box. In this simulation, the geometry normals are used to apply the boundary conditions on all refracting surfaces. This is appropriate for the highest accuracy ray traces in single-physics simulations, where the geometry is not deformed.
|
|
1
|
|
2
|
|
3
|
Locate the Boundary Selection section. From the Selection list, choose Mirror surface (Primary Mirror).
|
|
1
|
|
2
|
|
3
|
Locate the Boundary Selection section. From the Selection list, choose Mirror surface (Secondary Mirror).
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
In the Lengths text field, type 0 17. This path length is sufficient to ensure that all rays reach the image plane.
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
In the Model Builder window, expand the Results>Ray Diagram>Ray Trajectories 1 node, then click Color Expression 1.
|
|
2
|
|
3
|
In the Expression text field, type at('last',gop.rrel). This is the radial coordinate relative to the centroid at the image plane for each release feature.
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
In the Expression text field, type at(0,gop.rrel). This is the radial coordinate relative to the centroid at the entrance pupil for each ray release.
|
|
4
|