
|
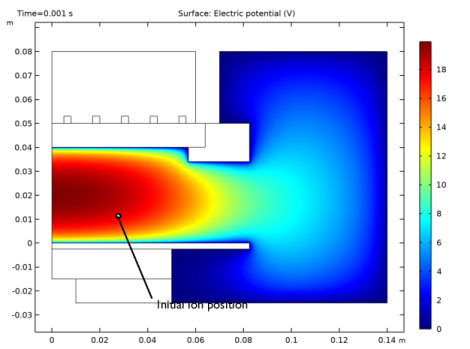

|
1
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
Find the Physics interfaces in study subsection. In the table, clear the Solve check boxes for Plasma (plas) and Magnetic Fields (mf).
|
|
3
|
|
4
|
|
5
|
|
1
|
In the Model Builder window, expand the Component 1 (comp1) node, then click Charged Particle Tracing (cpt).
|
|
2
|
|
3
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
Locate the Definition section. In the Expression text field, type 1.15e-18*x^(-0.1)*(1+0.015/x)^0.6.
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
Locate the Definition section. In the Expression text field, type 2e-19/(x^(0.5)*(1+x))+3e-19*x/(1+x/3)^(2.3).
|
|
4
|
|
5
|
|
1
|
In the Model Builder window, under Component 1 (comp1)>Charged Particle Tracing (cpt) click Particle Properties 1.
|
|
2
|
|
3
|
|
4
|
|
1
|
|
3
|
|
4
|
|
5
|
|
6
|
Locate the Advanced Settings section. Select the Use piecewise polynomial recovery on field check box.
|
|
1
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
1
|
|
2
|
|
3
|
|
4
|
Click to expand the Values of Dependent Variables section. Find the Values of variables not solved for subsection. From the Settings list, choose User controlled.
|
|
5
|
|
6
|
|
7
|
|
1
|
|
2
|
In the Settings window for 1D Plot Group, type Ion Energy Distribution Function in the Label text field.
|
|
3
|
|
4
|
|
1
|
|
2
|
In the Settings window for Histogram, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1 (comp1)>Charged Particle Tracing>Velocity and energy>cpt.Ep - Particle kinetic energy - J.
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
In the Settings window for 1D Plot Group, type Ion Angular Distribution Function in the Label text field.
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
In the associated text field, type Ion angle of incidence (deg).
|
|
5
|
|
1
|
|
2
|
In the Settings window for 2D Plot Group, type Ion Angular Energy Distribution Function in the Label text field.
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
Select the Description check box.
|
|
6
|
In the associated text field, type Angle of incidence (deg).
|
|
7
|
|
8
|
|
9
|
|
10
|
|
11
|
|
12
|
|
1
|
|
2
|
|
3
|