
|
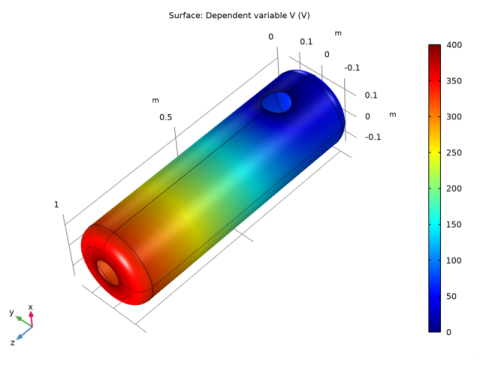
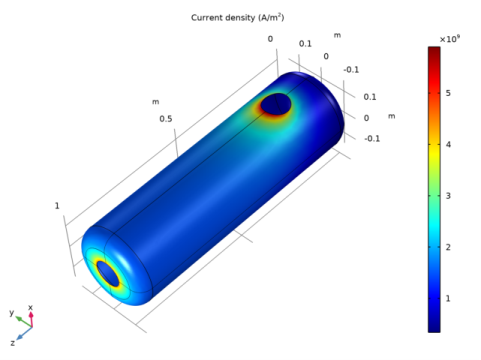
|
1
|
|
2
|
In the Select Physics tree, select Mathematics>PDE Interfaces>Lower Dimensions>Coefficient Form Boundary PDE (cb).
|
|
3
|
Click Add.
|
|
4
|
In the Dependent variables table, enter the following settings:
|
|
5
|
Click
|
|
6
|
|
7
|
Click
|
|
1
|
|
2
|
|
1
|
|
2
|
Browse to the model’s Application Libraries folder and double-click the file shell_diffusion_geom_sequence.mph.
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
Click
|
|
6
|
|
7
|
Click OK.
|
|
8
|
|
9
|
In the Source term quantity table, enter the following settings:
|
|
1
|
In the Model Builder window, under Component 1 (comp1)>Coefficient Form Boundary PDE (cb) click Coefficient Form PDE 1.
|
|
2
|
|
3
|
|
4
|
|
1
|
|
3
|
In the Settings window for Dirichlet Boundary Condition, locate the Dirichlet Boundary Condition section.
|
|
4
|
|
1
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
Select the Description check box.
|
|
7
|
In the associated text field, type Current field (-sigma*VTx, -sigma*VTy, -sigma*VTz).
|
|
8
|
|
9
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|