
|
|
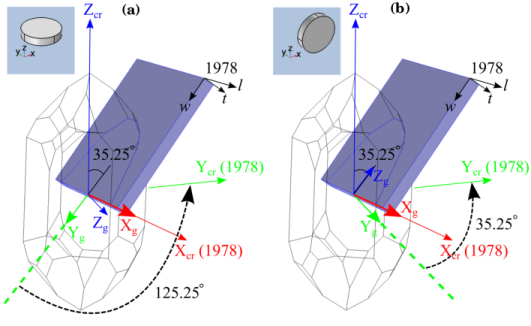
When defining the material properties of quartz, the orientation of the crystal axes X, Y, and Z with respect to the crystal differs between the 1978 IEEE standard and the 1949 IRE standard, as shown in Figure 3. (In the figure the crystal axes X, Y, and Z are labeled as Xcr, Ycr, and Zcr for clarity.) A consequence of this is that both the material property matrices and the crystal cut differ between the two standards. Table 1 summarizes the signs for the important matrix elements under the two conventions. Table 2 shows the different definitions of the crystal cuts under the two conventions.
|
|
1
|
The IRE or IEEE standard defines the relationship between the crystal axes (Xcr, Ycr, Zcr) and the plate axes (l, w, t).
|
|
2
|
When creating a COMSOL Multiphysics model, we draw the plate in the geometry window, thereby implicitly defines the relationship between the plate axes (l, w, t) and the global axes (Xg, Yg, Zg). If the plate is oriented differently in the model geometry, then this relationship will also be different.
|
|
3
|
Using the two relationships above, we can determine the relationship between the crystal axes (Xcr, Ycr, and Zcr) and the global axes (Xg, Yg, and Zg).
|
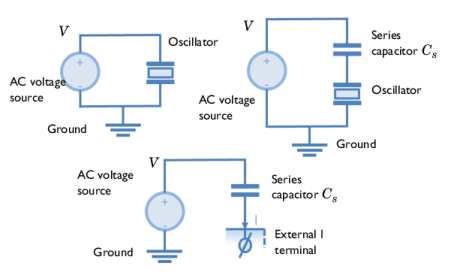
|
1
|
|
2
|
In the Select Physics tree, select Structural Mechanics>Electromagnetics-Structure Interaction>Piezoelectricity>Piezoelectricity, Solid.
|
|
3
|
Click Add.
|
|
4
|
Click
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
Click Browse.
|
|
4
|
Browse to the model’s Application Libraries folder and double-click the file thickness_shear_quartz_oscillator_mesh.mphbin.
|
|
5
|
Click Import.
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
In the Model Builder window, under Component 1 (comp1)>Solid Mechanics (solid) click Piezoelectric Material 1.
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
1
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
5
|
|
6
|
|
1
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
1
|
|
2
|
|
4
|
|
5
|
|
1
|
|
2
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
6
|
Locate the Physics and Variables Selection section. In the table, clear the Solve for check box for Electrical Circuit (cir).
|
|
7
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
In the Settings window for Surface, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1 (comp1)>Solid Mechanics>Displacement>solid.disp - Displacement magnitude - m.
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
1
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
6
|
Locate the Physics and Variables Selection section. Select the Modify model configuration for study step check box.
|
|
7
|
In the Physics and variables selection tree, select Component 1 (comp1)>Electrostatics (es)>Terminal 2.
|
|
8
|
Click
|
|
9
|
Locate the Values of Dependent Variables section. Find the Store fields in output subsection. From the Settings list, choose For selections.
|
|
10
|
|
11
|
|
12
|
Click OK.
|
|
1
|
|
2
|
|
3
|
Click
|
|
5
|
|
6
|
|
7
|
|
8
|
|
1
|
|
2
|
In the Settings window for 1D Plot Group, type Mechanical response, Parametric in the Label text field.
|
|
3
|
|
4
|
|
1
|
In the Model Builder window, expand the Mechanical response, Parametric node, then click Point Graph 1.
|
|
2
|
|
3
|
|
4
|