PDF
Normal Modes of a Biased Resonator — 2D
Introduction
Silicon micromechanical resonators have long been used for designing sensors and are now becoming increasingly important as oscillators in the consumer electronics market. In this sequence of models, a surface micromachined MEMS resonator, designed as part of a micromechanical filter, is analyzed in detail. The resonator is based on that developed in Ref. 1.
This model performs a modal analysis on the resonator, with and without an applied DC bias. The analysis begins from the stationary analysis performed in the accompanying model Stationary Analysis of a Biased Resonator — 2D; please review this model first.
Model Definition
The geometry, fabrication, and operation of the device are discussed for the “Stationary Analysis of a Biased Resonator” model.
This model performs a modal analysis on the structure, with and without applied DC voltage biases of different magnitudes. The bias already exists as a parameter in the model so the prestressed eigenfrequency solver needs no adjustment to the physics settings. To compute the unbiased eigenfrequency, the solver settings are adjusted to solve only the structural mechanics problem.
Results and Discussion
Figure 1 shows the mode shapes for the resonator under different bias conditions.
The mode shape does not change significantly with applied bias and the first three modes have the expected shapes for a clamped-clamped beam. The frequency of the fundamental is reduced significantly by the applied bias, an effect known as spring softening (the response of higher-order modes was not computed as a function of applied bias).
Figure 1: Mode shapes for the resonator under different bias conditions . The mode frequencies are indicated in the figure. The colors visualize the relative y-displacement magnitude.
The spring softening effect can be seen in detail in Figure 2. A clear decrease in the resonant frequency is evident with increasing bias voltage. This figure should be compared with Figure 16 of Ref. 1, where the same effect is apparent.
Figure 2: Mode frequency shown against the applied DC voltage bias. The spring softening effect is evident. Compare with Fig. 16 of Ref. 1.
Notes About the COMSOL Implementation
This model excludes certain dependent variables from the solver settings in order to compute the unbiased eigenfrequency. By not computing for the electric potential or the displacement of the air domains, the model is equivalent to a pure solid mechanics problem, solved in the absence of external forces. Excluding dependent variables in the solver in this manner can be useful for debugging models as well as for computing uncoupled problems in this manner.
Reference
1. F.D. Bannon III, J.R. Clark, and C. T.-C. Nguyen, “High-Q HF Microelectromechanical Filters”, IEEE Journal of Solid State Circuits, vol. 35, no. 4, pp. 512–526, 2000.
Application Library path: MEMS_Module/Actuators/biased_resonator_2d_modes
Modeling Instructions
Root
Open the existing stationary study (filename: biased_resonator_2d_basic.mph).
1
From the File menu, choose Open.
2
Browse to the model’s Application Libraries folder and double-click the file biased_resonator_2d_basic.mph.
Add an unbiased eigenfrequency study. The settings for this study need to be modified so that only the structural part of the problem is solved.
Add Study
1
In the Home toolbar, click  Add Study to open the Add Study window.
2
Go to the Add Study window.
3
Find the Studies subsection. In the Select Study tree, select Preset Studies for Selected Multiphysics>Eigenfrequency.
4
Click Add Study in the window toolbar.
5
In the Home toolbar, click  Add Study to close the Add Study window.
Study 2
Step 1: Eigenfrequency
1
In the Settings window for Eigenfrequency, locate the Study Settings section.
2
Select the Desired number of eigenfrequencies check box.
3
In the associated text field, type 3.
4
In the Model Builder window, right-click Study 2 and choose Rename.
5
In the Rename Study dialog box, type Unbiased Eigenfrequency in the New label text field.
6
Click OK.
Set up the solver to solve only for the solid mechanics variables.
Solution 2 (sol2)
1
In the Study toolbar, click  Show Default Solver.
2
In the Model Builder window, expand the Solution 2 (sol2) node, then click Dependent Variables 1.
3
In the Settings window for Dependent Variables, locate the General section.
4
From the Defined by study step list, choose User defined.
5
In the Model Builder window, expand the Unbiased Eigenfrequency>Solver Configurations>Solution 2 (sol2)>Dependent Variables 1 node, then click Electric potential (comp1.V).
6
In the Settings window for Field, locate the General section.
7
Clear the Solve for this field check box.
8
Clear the Store in output check box.
9
In the Model Builder window, click Spatial mesh displacement (comp1.spatial.disp).
10
In the Settings window for Field, locate the General section.
11
Clear the Solve for this field check box.
12
Clear the Store in output check box.
13
In the Model Builder window, click Unbiased Eigenfrequency.
14
In the Settings window for Study, locate the Study Settings section.
15
Clear the Generate default plots check box.
16
In the Study toolbar, click  Compute.
Set the dataset to be in the material frame for postprocessing. This allows the use of the deformation plot attribute.
Results
Unbiased Eigenfrequency/Solution 2 (sol2)
1
In the Model Builder window, expand the Results>Datasets node, then click Unbiased Eigenfrequency/Solution 2 (sol2).
2
In the Settings window for Solution, locate the Solution section.
3
From the Frame list, choose Material  (X, Y, Z).
Plot the mode shapes.
Unbiased Modes
1
In the Home toolbar, click  Add Plot Group and choose 2D Plot Group.
2
In the Settings window for 2D Plot Group, locate the Data section.
3
From the Dataset list, choose Unbiased Eigenfrequency/Solution 2 (sol2).
4
Right-click 2D Plot Group 3 and choose Rename.
5
In the Rename 2D Plot Group dialog box, type Unbiased Modes in the New label text field.
6
Click OK.
Surface 1
1
Right-click Unbiased Modes and choose Surface.
2
In the Settings window for Surface, locate the Expression section.
3
In the Expression text field, type v.
Deformation 1
1
Right-click Surface 1 and choose Deformation.
2
In the Unbiased Modes toolbar, click  Plot.
3
Click the  Zoom Extents button in the Graphics toolbar.
Compare the mode shapes with those shown in Figure 1 for all the modes computed. To switch between the modes click Unbiased Modes and choose a different value from the Eigenfrequency list.
Root
Add a Eigenfrequency, Prestressed study.
Add Study
1
In the Home toolbar, click  Add Study to open the Add Study window.
2
Go to the Add Study window.
3
Find the Studies subsection. In the Select Study tree, select Preset Studies for Selected Physics Interfaces>Solid Mechanics>Eigenfrequency, Prestressed.
4
Click Add Study in the window toolbar.
5
In the Home toolbar, click  Add Study to close the Add Study window.
Biased Eigenfrequency
1
In the Model Builder window, right-click Study 3 and choose Rename.
2
In the Rename Study dialog box, type Biased Eigenfrequency in the New label text field.
3
Click OK.
Create a parametric sweep over DC bias voltage.
Parametric Sweep
1
In the Study toolbar, click  Parametric Sweep.
2
In the Settings window for Parametric Sweep, locate the Study Settings section.
3
Click  Add.
4
Click  Range.
5
In the Range dialog box, type 5 in the Start text field.
6
In the Step text field, type 5.
7
In the Stop text field, type 45.
8
Click Add.
Solve for only the first eigenfrequency.
Step 2: Eigenfrequency
1
In the Model Builder window, click Step 2: Eigenfrequency.
2
In the Settings window for Eigenfrequency, locate the Study Settings section.
3
Select the Desired number of eigenfrequencies check box.
4
In the associated text field, type 1.
Disable the default plots.
5
In the Model Builder window, click Biased Eigenfrequency.
6
In the Settings window for Study, locate the Study Settings section.
7
Clear the Generate default plots check box.
8
In the Study toolbar, click  Compute.
Results
Biased Eigenfrequency/Parametric Solutions 1 (sol5)
1
In the Model Builder window, under Results>Datasets click Biased Eigenfrequency/Parametric Solutions 1 (sol5).
2
In the Settings window for Solution, locate the Solution section.
3
From the Frame list, choose Material  (X, Y, Z).
Biased Modes
1
In the Model Builder window, right-click Unbiased Modes and choose Duplicate.
2
Right-click Unbiased Modes 1 and choose Rename.
3
In the Rename 2D Plot Group dialog box, type Biased Modes in the New label text field.
4
Click OK.
5
In the Settings window for 2D Plot Group, locate the Data section.
6
From the Dataset list, choose Biased Eigenfrequency/Parametric Solutions 1 (sol5).
7
In the Biased Modes toolbar, click  Plot.
8
Click the  Zoom Extents button in the Graphics toolbar.
Confirm the mode shape is similar to the unbiased fundamental mode.
Create a plot of eigenfrequency versus applied DC voltage.
Eigenfrequency vs. DC voltage
1
In the Home toolbar, click  Add Plot Group and choose 1D Plot Group.
2
In the Settings window for 1D Plot Group, locate the Data section.
3
From the Dataset list, choose Biased Eigenfrequency/Parametric Solutions 1 (sol5).
4
Right-click 1D Plot Group 5 and choose Rename.
5
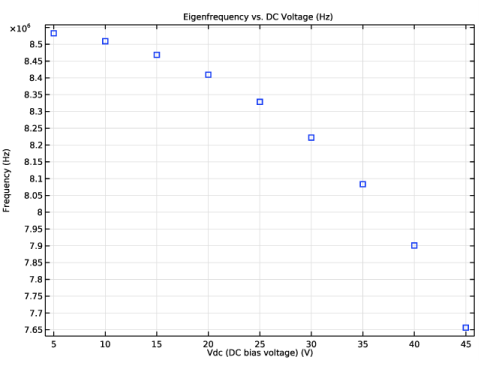
In the Rename 1D Plot Group dialog box, type Eigenfrequency vs. DC voltage in the New label text field.
6
Click OK.
Point Graph 1
1
Right-click Eigenfrequency vs. DC voltage and choose Point Graph.
2
In the Settings window for Point Graph, locate the Selection section.
3
Click  Paste Selection.
4
In the Paste Selection dialog box, type 1 in the Selection text field.
5
Click OK.
6
In the Settings window for Point Graph, locate the y-Axis Data section.
7
In the Expression text field, type solid.freq.
8
Locate the x-Axis Data section. From the Axis source data list, choose Outer solutions.
9
Click to expand the Title section. From the Title type list, choose Custom.
10
Find the Type and data subsection. Clear the Type check box.
11
Clear the Description check box.
12
Find the User subsection. In the Prefix text field, type Eigenfrequency vs. DC Voltage.
13
Click to expand the Coloring and Style section. Find the Line style subsection. From the Line list, choose None.
14
Find the Line markers subsection. From the Marker list, choose Square.
15
From the Positioning list, choose In data points.
Compare this plot with that in Figure 2. Note the spring softening effect.
16
In the Eigenfrequency vs. DC voltage toolbar, click  Plot.
17
Click the  Zoom Extents button in the Graphics toolbar.