Mixed Diffuse-Specular Radiation Benchmark

This tutorial shows how to use the Mathematical Particle Tracing interface to simulate radiative heat transfer with mixed diffuse-specular reflection between surfaces in an enclosure. This application is separated in two parts. The first part compares the heat fluxes computed by the Mathematical Particle Tracing interface with the exact solution for two identical infinitely long parallel gray plates under mixed diffuse-specular reflection at constant temperature. The second part couples the Mathematical Particle Tracing interface with the Heat Transfer in Solids interface for the parallel plate geometry but with different characteristics and spatially varying temperatures.

Introduction

Gray surfaces in an enclosure can reflect radiant energy specularly, that is, they reflect light like a mirror. This is particularly true for optically smooth surfaces like clean metals and glassy materials. For these materials the reflectance of a surface can be adequately represented by a combination of a diffuse and a specular component.

Following Ref. 1, the reflectance ρ of a surface can be expressed as

Where ρs and ρd are respectively the specular and diffusive reflectance of the surface, and where the symbols ε and α are the emissivity and absorptivity of the surface.

The heat flux q at surfaces in an enclosure is then defined by:

Where J is the surface radiosity

Eb is the blackbody emissive power

and H is the irradiance

The latter expression depends on the external irradiation

and on the differential specular view factor

For more details on the terminology see Ref. 1.

Model Definition

The model uses the Mathematical Particle Tracing interface to model radiative heat transfer using a discrete transfer method. The heat flux at each boundary element on the surface is computed by sending rays outward from the surface to query the temperatures of other surfaces in the geometry. The following three features are used:

The Inlet feature is used to determine the irradiance of a surface by backward ray tracing. Particles, which represent rays, are released uniformly on the inlet surfaces using a constant velocity. Particles are release uniformly within a hemisphere in velocity space (in 3D) or a semicircle (in 2D) centered about the surface normal.

In 2D the irradiance per ray Hij is defined as

where Eb is the blackbody emissive power of the surface at which the ray arrives and θ is the acute angle between the initial particle velocity vector and the surface normal. The angle Δθ is the plane angle subtended by each ray. The additional factor 1/2 is used for normalization purposes and compensates for the use of cos(θ) to assign weights to different rays based on their angles of incidence; this is validated by the integral

where Δθ is the solid angle subtended by each ray. The validity of the correction factor 1/π is confirmed by the integral

The Nonlocal Accumulator subnode, which can be added to the Inlet node, transmits the value of a variable at the particle’s current position and communicates this information back to the mesh element from which the particle was released, where it can be used to change the value of a dependent variable. With the Nonlocal Accumulator it is possible to map the irradiance per ray to the mesh elements from which the rays are initially released. For a mesh element i, the irradiance is

Where N is the number of rays released from the mesh element i.

The Wall node is used to make particles freeze, reflect diffusely, or reflect specularly at boundaries. The irradiance per ray is only set to a nonzero value when a ray is frozen to the wall, so the study must continue for enough time for all particles to freeze. The time a ray (particle) take to be absorbed depends on the emittance and reflectance of the walls.

The following algorithm is implemented to fulfill the first equation above:

Generate a random number rn1 between 0 and 1.

If rn1 > ρ the ray is absorbed (Freeze condition).

If rn1 ≤ ρ generation of a second random number rn2 between 0 and 1.

If rn2 < ρs ⁄ ρ the ray undergoes specular reflection (Bounce condition).

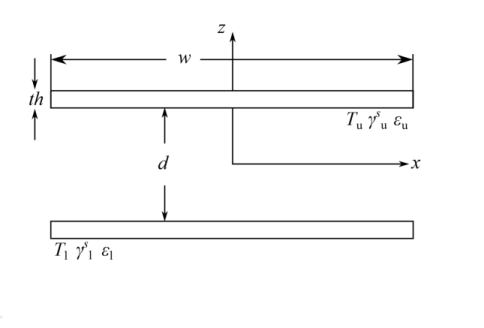
If rn2 ≥ ρs ⁄ ρ the ray undergoes diffuse reflection with a probability distribution based on Knudsen’s cosine law (Diffuse scattering condition).

The model is separated into two parts.

In the first part, we compare the exact analytical solution to the numerical result obtained with the Mathematical Particle Tracing interface.

This computes the heat flux at the surfaces of two identical infinitely long (out-of-plane on Figure 1) parallel plates placed in cold surroundings with mixed diffuse-specular radiation at their surfaces.

The geometry is illustrated in Figure 1. For the benchmark model the lower and upper plates have the same temperature Tl = Tu = T, the same emittance εl = εu = ε, and the same probability of specular reflection γl = γu = γ.

Using symmetries, it is possible to determine the heat flux (ql = qu = q) on the lower and upper plates using the following analytical solution see Ref. 1.

Where ξ = x ⁄ d, W = w ⁄ d and Ψ = q ⁄ Eb. The heat flux can be computed using numerical quadrature; a typical solution is presented on Figure 2.

Figure 1: Schematics of the problem. The width of the plates are w = 10 cm, their thickness th = w/20, and the distance between the plates set to d = 10 cm. The temperature, emittance and probability of specular reflection are equal for both plates and respectively set to T = 300 K, ε = 0.6, and γs = 0.8.

The second part keeps the parallel plates arrangement (same geometry) but changes the surface properties and couple the radiation model developed above to the Heat Transfer in Solids interface. Table 1 displays the surface parameters used for this part of the application.

Table 1: Surface parameters
Surfaces	ε	γs
Surrounding	1	0
Lower plate	0.9	0.1
Upper plate	0.6	0.8

For this model, the upper plate, made of copper, is heated locally from the top. The lower plate, made of quartz, is heated by the radiation emitted from the upper plate and cooled by natural convection on the bottom surface. The plates’ surrounding temperature is set to 300 K.

Results and Discussion

Figure 2 shows a comparison of the normalized heat flux at the plate’s surfaces for the exact and ray tracing solutions (benchmark model). A good agreement is observed between the curves. Because the Diffuse scattering wall condition is stochastic in nature, the solutions on the top and bottom surfaces differ slightly from each other and from the exact solution.

When the heat source computed using the Mathematical Particle Tracing interface is coupled to the Heat Transfer in Solids interface, the temperature field shown in Figure 3 is obtained. The temperature on the surface of the bottom plate is plotted in Figure 4. Figure 5 displays the normalized heat flux at the top of the lower plate (blue) and at the bottom of the upper plate (green).

Figure 2: Normalized heat flux at the top of the lower plate (blue) and at the bottom of the upper plate (green) for T = 300 K, ε = 0.6, γs = 0.8 and w/d = 1. The black circles represent the exact solution (the same for both surfaces) obtained from numerical quadrature see Ref. 1.

Figure 3: Temperature at the surface of the plates for the coupled model.

Figure 4: Temperature at the surface of the lower plate for the coupled model.

Figure 5: Heat flux at the top of the lower plate (blue) and at the bottom of the upper plate (green) for the coupled model.

Notes About the COMSOL Implementation

This 3D model uses a bounce boundary condition to simulate the effect of infinitely long plates (symmetry conditions).

An auxiliary dependent variable is necessary to define the release angle of each ray.

The second study consists of two study steps, a Stationary study step to compute the temperature and a Time Dependent study step to compute the particle trajectories and radiative heat flux. A self-consistent solution is obtained via an iterative process in which a For-End For loop is used to alternate between the stationary and time-dependent solvers. The loop should be continued until the change in temperature at each successive iteration is negligibly small. For this application, an acceptable self-consistent solution is obtained in three iterations.

Reference

1. M. F. Modest, Radiative Heat Transfer, 2nd. ed., Academic Press, 2003.

Heat_Transfer_Module/Thermal_Radiation/parallel_plates_diffuse_specular

Modeling Instructions

From the menu, choose .

New

In the window, click

Model Wizard

In the window, click

In the tree, select .

Click .

Click

In the tree, select .

Click

Global Definitions

Parameters 1

In the window, under click .

In the window for , locate the section.

In the table, enter the following settings:


Name	Expression	Value	Description
w	10[cm]	0.1 m	Width of the plates
d	10[cm]	0.1 m	Distance between the plates
l	2*w	0.2 m	Length of the plates
th	w/20	0.005 m	Thickness of the plates
M	20	20	Number of ray bundles along the width of the plates (number of elements)
N	300	300	Number of rays per bundle
Delta_theta	2*pi/N	0.020944	Solid angle subtended per ray
T0	300[K]	300 K	Room temperature

Geometry 1

Block 1 (blk1)

In the toolbar, click

In the window for , locate the section.

In the text field, type 2*w.

In the text field, type l.

In the text field, type 2*w.

Locate the section. From the list, choose .

Block 2 (blk2)

In the toolbar, click

In the window for , locate the section.

In the text field, type w.

In the text field, type l.

In the text field, type th.

Locate the section. From the list, choose .

In the text field, type -(d+th)/2.

Block 3 (blk3)

Right-click and choose .

In the window for , locate the section.

In the text field, type (d+th)/2.

Click the

button in the toolbar in order to see the entire geometry.

Work Plane 1 (wp1)

In the toolbar, click

Partition the lower upper plate in two sections. The lines created by the partition will be used to display the heat flux across the plates’ width.

In the window for , locate the section.

From the list, choose .

Partition Objects 1 (par1)

In the toolbar, click

and choose .

Click in the window and then press Ctrl+A to select all objects.

In the window for , locate the section.

From the list, choose .

In the toolbar, click

Define a selection list for the surrounding, lower and upper plate.

Definitions

Surrounding

In the toolbar, click

In the window for , type Surrounding in the text field.

Locate the section. From the list, choose .

Select Boundaries 1–5, 7–9, 32, and 33 only.

Lower Plate

In the toolbar, click

In the window for , type Lower Plate in the text field.

Locate the section. From the list, choose .

Select Boundaries 10–13, 18, 20, 21, 26, 28, and 30 only.

Upper Plate

In the toolbar, click

In the window for , type Upper Plate in the text field.

Locate the section. From the list, choose .

Select Boundaries 14–17, 22, 24, 25, 27, 29, and 31 only.

Define the model variables.

Definitions

In the toolbar, click

In the window for , type Definitions in the text field.

Locate the section. In the table, enter the following settings:


Name	Expression	Unit	Description
H_ij	nojac(1/pisigma_constbndenv(Ts)^4abs(cos(theta_emit))Delta_theta)		Irradiance per ray
Eb	sigma_const*Ts^4		Blackbody emissive power
rho	1-epsilon		Surface reflectance
q	-epsilon*(Eb-pt.inl1.nacc1.rpi)		Heat flux

Surrounding: Study 1

In the toolbar, click

In the window for , type Surrounding: Study 1 in the text field.

Locate the section. From the list, choose .

From the list, choose .

Locate the section. In the table, enter the following settings:


Name	Expression	Unit	Description
Ts	0[K]	K	Temperature of the surrounding
epsilon	1		Emittance of the surrounding
gamma_s	0		Probability of specular reflection

Lower Plate: Study 1

In the toolbar, click

In the window for , type Lower Plate: Study 1 in the text field.

Locate the section. From the list, choose .

From the list, choose .

Locate the section. In the table, enter the following settings:


Name	Expression	Unit	Description
Ts	T0	K	Temperature of the lower plate
epsilon	0.6		Emittance of the lower plate
gamma_s	0.8		Probability of specular reflection

Upper Plate: Study 1

In the toolbar, click

In the window for , type Upper Plate: Study 1 in the text field.

Locate the section. From the list, choose .

From the list, choose .

Locate the section. In the table, enter the following settings:


Name	Expression	Unit	Description
Ts	T0	K	Temperature of the upper plate
epsilon	0.6		Emittance of the upper plate
gamma_s	0.8		Probability of specular reflection

Surrounding: Study 2

In the toolbar, click

In the window for , type Surrounding: Study 2 in the text field.

Locate the section. From the list, choose .

From the list, choose .

Locate the section. In the table, enter the following settings:


Name	Expression	Unit	Description
Ts	T0	K	Temperature of the surrounding
epsilon	1		Emittance of the surrounding
gamma_s	0		Probability of specular reflection

Lower Plate: Study 2

In the toolbar, click

In the window for , type Lower Plate: Study 2 in the text field.

Locate the section. From the list, choose .

From the list, choose .

Locate the section. In the table, enter the following settings:


Name	Expression	Unit	Description
Ts	T		Temperature of the lower plate
epsilon	0.9		Emittance of the lower plate
gamma_s	0.1		Probability of specular reflection

Upper Plate: Study 2

In the toolbar, click

In the window for , type Upper Plate: Study 2 in the text field.

Locate the section. From the list, choose .

From the list, choose .

Locate the section. In the table, enter the following settings:


Name	Expression	Unit	Description
Ts	T		Temperature of the upper plate
epsilon	0.6		Emittance of the upper plate
gamma_s	0.8		Probability of specular reflection

Now define the mathematical particle tracing model. Set the to zero and avoid allocating unnecessary degrees of freedom to the problem.

Mathematical Particle Tracing (pt)

In the window, under click .

In the window for , locate the section.

In the text field, type 0.

Locate the section. Click

Select Domains 1 and 2 only.

Auxiliary Dependent Variable 1

In the toolbar, click

and choose .

Add an auxiliary dependent variable that will be used to compute the released angle of the particles.

In the window for , locate the section.

In the text field, type theta_emit.

Locate the section. Click

In the dialog box, type planeangle in the text field.

Click

In the tree, select .

Click .

Add an inlet to the surface to which we want to compute the flux, i.e. the lower and upper plate surfaces with the exception of the bottom surface of the lower plate and the top surface of the upper plate.

Inlet 1

In the toolbar, click

and choose .

Select Boundaries 10, 13, 14, 16, 18, 21, 22, 24, and 28–31 only.

In the window for , locate the section.

From the list, choose in order to have an equidistant distribution of rays.

Enter the number of rays per bundle in the field.

In the Nvel text field, type N.

Select the check box.

Specify the r vector as


0	t1
0	t2
1	n

Enter the built-in variable for the release angle in the field.

Locate the section. In the thetaemit0 text field, type pt.inl1.thetarel.

Add a nonlocal accumulator to map the computed irradiance per ray to the constant discontinuous Lagrange elements associated to the release sites (in this case at the center of the mesh elements).

Nonlocal Accumulator 1

In the toolbar, click

and choose .

In the window for , locate the section.

From the list, choose .

In the R text field, type H_ij.

From the list, choose .

Locate the section. Click

In the dialog box, type radiativeintensity in the text field.

Click

In the tree, select .

Click .

Add the bounce boundary condition at the extremities of the domain (symmetry condition). Note that the effect of temperature and emittance of the boundary set in the surrounding variables have no effect of the computation as the walls are, here, purely specular.

Wall 2

In the toolbar, click

and choose .

Select Boundaries 2 and 9 only.

In the window for , locate the section.

From the list, choose .

Select the remaining wall boundaries and set the probability of diffuse and specular reflection as well as the probability of absorption of the rays (rho). This wall boundary condition computes the probability of specular reflection (bounce otherwise Knudsen cosine law) if the ray has not been absorbed before. The probability of absorption is entered as rho in the field of the section.

Wall 3

In the toolbar, click

and choose .

Select Boundaries 1, 3–5, 7, 8, 10, 12–14, 16–18, 20–22, 24, 25, and 28–33 only.

In the window for , locate the section.

From the list, choose .

In the γs text field, type gamma_s.

Locate the section. From the list, choose .

In the γ text field, type rho.

To save on computation time, create a simple mesh on one extremity of the domain and sweep it over the entire domain using the swept mesh feature.

Mesh 1

Mapped 1

In the toolbar, click

and choose .

Select Boundaries 11 and 15 only.

Distribution 1

In the toolbar, click

Select Edges 16, 18, 21, and 23 only.

In the window for , locate the section.

In the text field, type M.

Distribution 2

In the toolbar, click

Select Edges 14, 19, 40, and 43 only.

In the window for , locate the section.

In the text field, type 1.

Free Triangular 1

In the toolbar, click

and choose .

Select Boundary 2 only.

Click the

button in the toolbar.

Swept 1

In the toolbar, click

In the window for , click

Generate the default solver sequence and enter a proper maximum time step for the time dependent solver. The particles must travel a distance lower than the distance between the walls for a given time step.

Study 1

Solution 1 (sol1)

In the toolbar, click

In the window, expand the node, then click .

In the window for , click to expand the section.

From the list, choose .

In the text field, type 0.01.

Enter 1.5 s as the final time step. This will give enough time for the majority of the particle to freeze.

Step 1: Time Dependent

In the window, click .

In the window for , locate the section.

In the text field, type 0,1.5.

Select the boundary definitions for the first study.

Locate the section. Select the check box.

In the tree, select .

Click

In the tree, select .

Click

In the tree, select .

Click

In the window, click .

In the window for , locate the section.

Clear the check box.

In the toolbar, click

Results

Load the heat flux data computed by Gauss quadrature. These data represent an exact solution of the model.

epsilon=0.6, gamma_s=0.8

In the window, expand the node.

Right-click and choose .

In the window for , type epsilon=0.6, gamma_s=0.8 in the text field.

Locate the section. Click .

Browse to the model’s Application Libraries folder and double-click the file parallel_plates_diffuse_specular_data.txt.

Table

Go to the window.

Results

epsilon=0.6, gamma_s=0.8

In the window, click .

In the window for , click

Validation

In the toolbar, click

Generate the heat flux comparison. By symmetry, the heat flux at the upper and lower plate should be the same.

In the window for , type Validation in the text field.

Locate the section. From the list, choose .

Line Graph 1

In the toolbar, click

In the window for , locate the section.

In the text field, type q/(epsilon*Eb).

Select Edge 28 only.

Locate the section. From the list, choose .

In the text field, type x/w.

Click to expand the section. Select the check box.

From the list, choose .

In the table, enter the following settings:


Legends
Lower plate

Click to expand the section. From the list, choose .

Line Graph 2

Right-click and choose .

In the window for , locate the section.

In the table, enter the following settings:


Legends
Upper plate

Locate the section. Select the

toggle button.

Click

Select Edge 31 only.

Validation

In the window, click .

Table Graph 1

In the toolbar, click

In the window for , locate the section.

Find the subsection. From the list, choose .

From the list, choose .

Find the subsection. From the list, choose .

From the list, choose .

Click to expand the section. Select the check box.

From the list, choose .

In the table, enter the following settings:


Legends
Gauss quadrature

In the toolbar, click

Now add a interface to the model. Here we are going to couple the radiative heat transfer to the heat transfer in the plates. For this model the top of the upper plate (copper) is heated by a local heat source with one side held at a constant temperature. The bottom of the lower plate (glass) is cooled by convection.

Add Physics

In the toolbar, click

to open the window.

Go to the window.

In the tree, select .

Find the subsection. In the table, clear the check box for .

Click in the window toolbar.

In the toolbar, click

to close the window.

Heat Transfer in Solids (ht)

In the window for , locate the section.

In the list, choose and .

Click

Select Domains 3–6 only.

Add the material properties to each plate.

Materials

Quartz

In the toolbar, click

In the window for , type Quartz in the text field.

Locate the section. Click

Select Domains 3 and 5 only.

Locate the section. In the table, enter the following settings:


Property	Variable	Value	Unit	Property group
Thermal conductivity	k_iso ; kii = k_iso, kij = 0	1.1[W/(m*K)]	W/(m·K)	Basic
Density	rho	2200[kg/m^3]	kg/m³	Basic
Heat capacity at constant pressure	Cp	480[J/(kg*K)]	J/(kg·K)	Basic

Copper

In the toolbar, click

In the window for , type Copper in the text field.

Select Domains 4 and 6 only.

Locate the section. In the table, enter the following settings:


Property	Variable	Value	Unit	Property group
Thermal conductivity	k_iso ; kii = k_iso, kij = 0	400[W/(m*K)]	W/(m·K)	Basic
Density	rho	8700[kg/m^3]	kg/m³	Basic
Heat capacity at constant pressure	Cp	385[J/(kg*K)]	J/(kg·K)	Basic