
|
|
5·10-3 Pa·s
|
1·10-3 Pa·s
|

|
1
|
|
2
|
Browse to the model’s Application Libraries folder and double-click the file double_pipe_heat_exchanger_preset.mph.
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
On the object imp1, select Boundary 27 only.
|
|
5
|
|
6
|
|
1
|
|
2
|
Select the object imp1 only.
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
On the object par1, select Boundary 40 only.
|
|
5
|
|
6
|
|
1
|
|
2
|
Select the object par1 only.
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
5
|
|
6
|
Click the Custom button.
|
|
7
|
|
8
|
|
9
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
1
|
In the Model Builder window, expand the Boundary Layers 1 node, then click Boundary Layer Properties.
|
|
2
|
In the Settings window for Boundary Layer Properties, locate the Geometric Entity Selection section.
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
In the Model Builder window, expand the Study 1>Solver Configurations>Solution 1 (sol1)>Stationary Solver 1 node, then click Segregated 1.
|
|
4
|
|
5
|
|
6
|
In the Model Builder window, expand the Study 1>Solver Configurations>Solution 1 (sol1)>Stationary Solver 1>AMG, fluid flow variables (spf) node, then click Multigrid 1.
|
|
7
|
|
8
|
|
9
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
Use the Graphics toolbox to get a satisfying view.
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
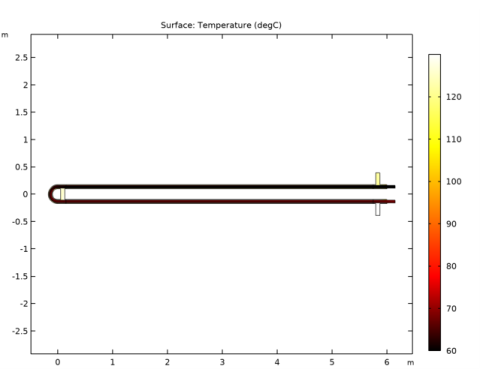
In the Settings window for 2D Plot Group, type Temperature (2D Center Plane) in the Label text field.
|
|
3
|
|
1
|
|
2
|
In the Settings window for Surface, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1 (comp1)>Heat Transfer in Fluids>Temperature>T - Temperature - K.
|
|
3
|
|
4
|
|
5
|
|
6
|
Use the Graphics toolbox to get a satisfying view.
|
|
1
|
|
2
|
In the Settings window for Global Evaluation, type Heat Transfer Coefficient in the Label text field.
|
|
3
|
Locate the Expressions section. In the table, enter the following settings:
|
|
4
|
Click
|
|
1
|
Go to the Table window.
|
|
1
|
|
2
|
In the Settings window for Surface Average, type Outlet Temperature, Transformer Oil in the Label text field.
|
|
3
|
|
4
|
Click Replace Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Heat Transfer in Fluids>Temperature>T - Temperature - K.
|
|
5
|
Locate the Expressions section. In the table, enter the following settings:
|
|
6
|
Click
|
|
1
|
|
2
|
In the Settings window for Surface Average, type Outlet Temperature, Engine Oil in the Label text field.
|
|
3
|
|
4
|
Click
|
|
5
|
Go to the Table window.
|
|
1
|
|
2
|
In the Settings window for Surface Average, type Inlet Pressure, Transformer Oil in the Label text field.
|
|
3
|
|
4
|
Click Replace Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Laminar Flow>Velocity and pressure>p - Pressure - Pa.
|
|
5
|
|
6
|
Go to the Table window.
|
|
1
|
|
2
|
In the Settings window for Surface Average, type Inlet Pressure, Engine Oil in the Label text field.
|
|
3
|
|
4
|
Click
|
|
5
|
Go to the Table window.
|