
|

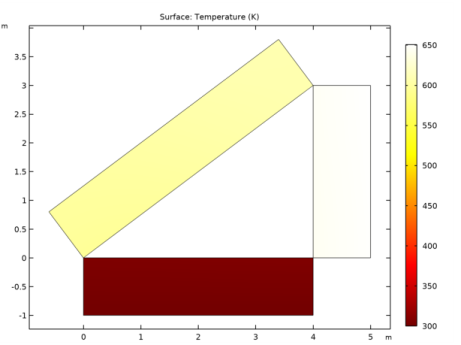
|
1
|
|
2
|
In the Select Physics tree, select Heat Transfer>Radiation>Heat Transfer with Surface-to-Surface Radiation.
|
|
3
|
Click Add.
|
|
4
|
Click
|
|
5
|
|
6
|
Click
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
1
|
In the Model Builder window, under Component 1 (comp1)>Heat Transfer in Solids (ht) click Initial Values 1.
|
|
2
|
|
3
|
|
1
|
|
3
|
|
4
|
|
1
|
|
3
|
|
4
|
|
1
|
|
3
|
|
4
|
|
1
|
|
1
|
In the Model Builder window, under Component 1 (comp1)>Surface-to-Surface Radiation (rad) click Diffuse Surface 1.
|
|
2
|
|
3
|
|
4
|
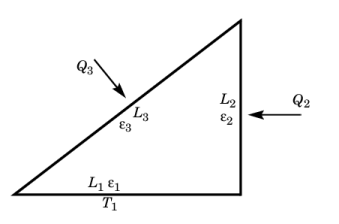
Locate the Surface Emissivity section. From the ε list, choose User defined. In the associated text field, type 0.8.
|
|
1
|
|
3
|
|
4
|
|
5
|
Locate the Surface Emissivity section. From the ε list, choose User defined. In the associated text field, type 0.4.
|
|
1
|
|
3
|
|
4
|
|
5
|
Locate the Surface Emissivity section. From the ε list, choose User defined. In the associated text field, type 0.6.
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
5
|
|
6
|
|
8
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
1
|
|
2
|
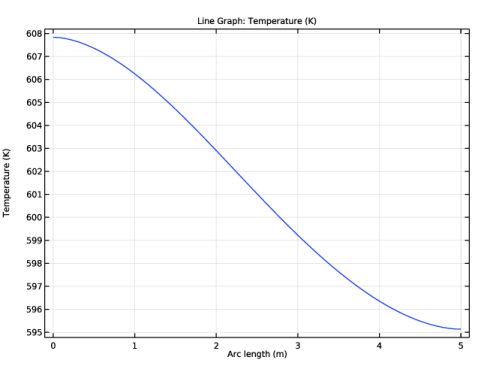
In the Settings window for 1D Plot Group, type Temperature Profile vs. Arc Length in the Label text field.
|
|
1
|
|
3
|
|
1
|
|
2
|
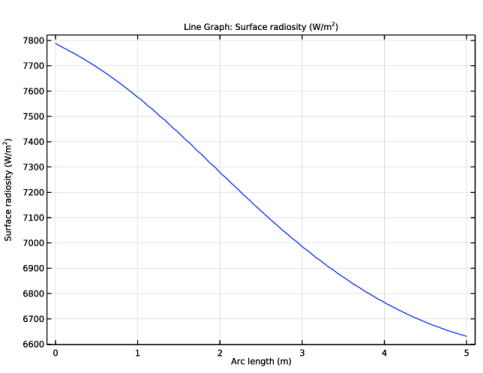
In the Settings window for 1D Plot Group, type Surface Radiosity Profile vs. Arc Length in the Label text field.
|
|
1
|
In the Model Builder window, expand the Surface Radiosity Profile vs. Arc Length node, then click Line Graph 1.
|
|
2
|
In the Settings window for Line Graph, click Replace Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Surface-to-Surface Radiation>Surface radiosity>rad.J - Surface radiosity - W/m².
|
|
3
|
|
1
|
|
3
|
In the Settings window for Line Integration, click Replace Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Heat Transfer in Solids>Boundary fluxes>ht.ndflux - Normal conductive heat flux - W/m².
|
|
4
|
Click
|
|
1
|
Go to the Table window.
|
|
1
|
|
3
|
|
5
|
Click
|
|
1
|
Go to the Table window.
|
|
1
|
|
3
|
|
5
|
Click
|
|
1
|
Go to the Table window.
|