PDF
Flexible and Smooth Strip Footing on Stratum of Clay
Model Definition
A typical verification example for geotechnical problems is a shallow stratum layer of clay, see Figure 1. In the example, a vertical load is applied on the clay stratum, and the static response as well as the collapse load are of interest.
Figure 1: Dimensions, boundary conditions, and pressure load for the stratum of clay.
Analysis Type
Yield Surface
Assume plane strain conditions, and model the clay with soil plasticity and the Drucker-Prager criterion.
The yield surface, F, for the Drucker-Prager criterion is given by
where I1 is the first stress invariant and J2 is the second deviatoric stress invariant.
The first stress invariant is defined using the trace of Cauchy stress tensor:
The second stress invariant is defined by
The second deviatoric stress invariant can be expressed using the first and the second stress invariants:
If two-dimensional plane strain conditions prevail, the Drucker-Prager criterion matches the Mohr-Coulomb criterion. For this case the material parameters α and k are given by the Cohesion c and the Angle of internal friction φ (Ref. 1)
Drucker-Prager criterion is the default choice for the Soil Plasticity feature, and the check box Match to Mohr-Coulomb criterion applies the aforementioned matching of the material parameters.
Under Soil Plasticity, it is also possible to use Mohr-Coulomb criterion
,
where σmax and σmin are the biggest and smallest principal stresses. The Mohr-Coulomb criterion defines an irregular hexagon pyramid in the principal stress space. Since this yield function gives rise to singularities in the derivatives of the yield function, the use of a non-associated flow rule with a Drucker-Prager plastic potential is chosen. This is done in the Plastic potential list, with the option Drucker-Prager matched at compressive meridian.
Flow Rule
The flow rule defines the relation between the plastic strain increment in a given direction and the current level of stress in the same direction. The relation reads
where λ is the plastic multiplier and Q is the plastic potential. If the yield surface, F, and the plastic potential, Q, are identical, that is, if F = Q, then it is called an associated flow rule, otherwise it is called a non-associated flow rule.
Soil Properties
•
Young’s modulus, E = 207 MPa, and Poisson’s ratio ν = 0.3.
•
Cohesion c = 69 MPa, and angle of internal friction φ = 20 degrees.
Constraints and Loads
•
The clay layer is supported by a rigid and perfectly rough base. Therefore, apply a fixed constraint on the lower horizontal boundary.
•
Model only the left half of the domain due to symmetry reasons. Use the symmetry boundary condition at the right vertical boundary.
•
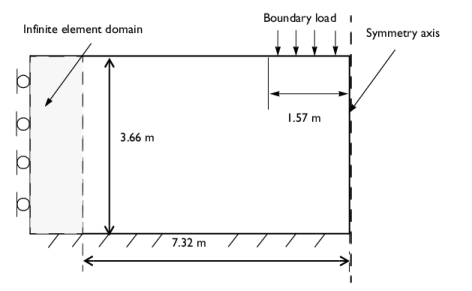
The stratum is subjected to a footing that you can consider to be flexible and smooth. The width of the strip footing is 3.14 m, see Figure 2. Gradually increase the footing pressure until the clay layer reaches the collapse load.
Figure 2: Boundary load applied to model the footing pressure
Infinite Element Domain
•
In order to mimic an infinite layer of soil, add an Infinite Element Domain. The scaling 1e3*root.mod1.dGeomChar means that the spatial variables in this domain are scaled thousand times the typical geometry length.
•
The left vertical boundary is perfectly smooth and a can be assumed to be of the roller type.
This example is adapted from Ref. 2.
Results and Discussion
You can study the load-displacement curves for both the Mohr-Coulomb and the Drucker-Prager criteria in Figure 3. The figure shows the applied footing pressure versus the centerline displacement (directly beneath the center of the footing) in the y direction. The lines show the load-displacement curves for the Mohr-Coulomb and Drucker-Prager criteria. The curves are identical up to 300 kPa because the whole domain is still within the elastic region. From that point when the pressure increases, the behavior diverges. Both curves reach the collapse load at approximately 1.1 MPa. The development of plastic strains in the soil at different stages of loading is shown in Figure 4.
Figure 3: Footing pressure versus vertical displacement for the Mohr-Coulomb and Drucker-Prager material models.
Figure 4: Evolution of the equivalent plastic strain on the clay layer during the parametric loading.
Notes About the COMSOL Implementation
Both the Mohr-Coulomb or Drucker-Prager criterion are predefined in the Soil Plasticity subfeature. The default Mohr-Coulomb criterion uses a nonassociated flow rule, with a plastic potential implemented as Drucker-Prager matched at compressive meridian. The yield function contains the first stress invariant, I1, and the second deviatoric stress invariant, J2, as well as the material property constants.
A suitable modeling technique in a case where the relation between the applied load and the displacement is highly nonlinear, is to use an algebraic equation that controls the applied pressure so that the model reaches the desired displacement increments. This is implemented using a Global Equation, and the parametric solver incrementally increases the displacement up to the desired vertical displacement.
References
1. W.F. Chen and E. Mizuno, Nonlinear Analysis in Soil Mechanics, Elsevier, 1990.
2. A. Mar. How To Undertake Finite Element Based Geotechnical Analysis, NAFEMS, 2002.
Application Library path: Geomechanics_Module/Soil/flexible_footing
Modeling Instructions
From the File menu, choose New.
New
In the New window, click  Model Wizard.
Model Wizard
1
In the Model Wizard window, click  2D.
2
In the Select Physics tree, select Structural Mechanics>Solid Mechanics (solid).
3
Click Add.
4
Click  Study.
5
In the Select Study tree, select General Studies>Stationary.
6
Click  Done.
Geometry 1
Rectangle 1 (r1)
1
In the Geometry toolbar, click  Rectangle.
2
In the Settings window for Rectangle, locate the Size and Shape section.
3
In the Width text field, type 7.32.
4
In the Height text field, type 3.66.
5
Click  Build Selected.
Add a rectangle to model the infinite element domain.
Rectangle 2 (r2)
1
In the Geometry toolbar, click  Rectangle.
2
In the Settings window for Rectangle, locate the Size and Shape section.
3
In the Width text field, type 7.32*0.1.
4
In the Height text field, type 3.66.
5
Locate the Position section. In the x text field, type -7.32*0.1.
6
Click  Build Selected.
Point 1 (pt1)
1
In the Geometry toolbar, click  Point.
2
In the Settings window for Point, locate the Point section.
3
In the x text field, type 7.32-1.57.
4
In the y text field, type 3.66.
5
Click  Build Selected.
Form Union (fin)
1
In the Model Builder window, click Form Union (fin).
2
In the Settings window for Form Union/Assembly, click  Build Selected.
Definitions
Infinite Element Domain 1 (ie1)
1
In the Definitions toolbar, click  Infinite Element Domain.
The infinite element domain is scaled by a factor of 1000.
2
Select Domain 1 only.
Global Definitions
Parameters 1
1
In the Model Builder window, under Global Definitions click Parameters 1.
2
In the Settings window for Parameters, locate the Parameters section.
3
In the table, enter the following settings:
Name
Expression
Value
Description
para
0
0
Prescribed displacement
Definitions
Use a nonlocal integration coupling to evaluate the displacement in the center of the applied pressure (Point 7).
Integration 1 (intop1)
1
In the Definitions toolbar, click  Nonlocal Couplings and choose Integration.
2
In the Settings window for Integration, locate the Source Selection section.
3
From the Geometric entity level list, choose Point.
4
Select Point 7 only.
Solid Mechanics (solid)
Linear Elastic Material 1
In the Model Builder window, under Component 1 (comp1)>Solid Mechanics (solid) click Linear Elastic Material 1.
Soil Plasticity 1
1
In the Physics toolbar, click  Attributes and choose Soil Plasticity.
2
In the Settings window for Soil Plasticity, locate the Soil Plasticity section.
3
Select the Match to Mohr-Coulomb criterion check box.
Linear Elastic Material 1
In the Model Builder window, click Linear Elastic Material 1.
Soil Plasticity 2
1
In the Physics toolbar, click  Attributes and choose Soil Plasticity.
2
In the Settings window for Soil Plasticity, locate the Soil Plasticity section.
3
From the Yield criterion list, choose Mohr-Coulomb.
Fixed Constraint 1
1
In the Physics toolbar, click  Boundaries and choose Fixed Constraint.
2
Select Boundaries 2 and 5 only.
Symmetry 1
1
In the Physics toolbar, click  Boundaries and choose Symmetry.
2
Select Boundary 8 only.
Roller 1
1
In the Physics toolbar, click  Boundaries and choose Roller.
2
Select Boundary 1 only.
Boundary Load 1
1
In the Physics toolbar, click  Boundaries and choose Boundary Load.
2
Select Boundary 7 only.
3
In the Settings window for Boundary Load, locate the Force section.
4
Specify the FA vector as
0
x
footing_pressure
y
5
Click the  Show More Options button in the Model Builder toolbar.
6
In the Show More Options dialog box, in the tree, select the check box for the node Physics>Equation-Based Contributions.
7
Click OK.
Global Equations 1
1
In the Physics toolbar, click  Global and choose Global Equations.
2
In the Settings window for Global Equations, locate the Global Equations section.
3
In the table, enter the following settings:
Name
f(u,ut,utt,t) (1)
Initial value (u_0) (1)
Initial value (u_t0) (1/s)
Description
footing_pressure
intop1(v)-para
0
0
 
4
Locate the Units section. Click  Select Dependent Variable Quantity.
5
In the Physical Quantity dialog box, type pressure in the text field.
6
Click  Filter.
7
In the tree, select General>Pressure (Pa).
8
Click OK.
9
In the Settings window for Global Equations, locate the Units section.
10
Click  Select Source Term Quantity.
11
In the Physical Quantity dialog box, type displacement in the text field.
12
Click  Filter.
13
In the tree, select General>Displacement (m).
14
Click OK.
Materials
Material 1 (mat1)
1
In the Model Builder window, under Component 1 (comp1) right-click Materials and choose Blank Material.
2
In the Settings window for Material, locate the Material Contents section.
3
In the table, enter the following settings:
Property
Variable
Value
Unit
Property group
Young’s modulus
E
207e6
Pa
Basic
Poisson’s ratio
nu
0.3
1
Basic
Cohesion
cohesion
69e3
Pa
Mohr-Coulomb
Angle of internal friction
internalphi
20[deg]
rad
Mohr-Coulomb
Mesh 1
1
In the Model Builder window, under Component 1 (comp1) click Mesh 1.
2
In the Settings window for Mesh, locate the Mesh Settings section.
3
From the Sequence type list, choose User-controlled mesh.
Size
1
In the Model Builder window, under Component 1 (comp1)>Mesh 1 click Size.
2
In the Settings window for Size, locate the Element Size section.
3
From the Predefined list, choose Finer.
Free Triangular 1
1
In the Model Builder window, click Free Triangular 1.
2
In the Settings window for Free Triangular, locate the Domain Selection section.
3
From the Geometric entity level list, choose Domain.
4
Select Domain 2 only.
Mapped 1
1
In the Mesh toolbar, click  Mapped.
Use a mapped mesh in the infinite element domain to improve convergence.
2
In the Settings window for Mapped, locate the Domain Selection section.
3
From the Geometric entity level list, choose Domain.
4
Select Domain 1 only.
5
Click  Build All.
The first study is parametric and solves the model assuming a Drucker-Prager criterion. The parameter represents the vertical displacement in the center of the applied pressure (Point 7). It runs from 0 to -32 mm with a step size of 0.5 mm.
Drucker-Prager criterion
1
In the Model Builder window, click Study 1.
2
In the Settings window for Study, type Drucker-Prager criterion in the Label text field.
Step 1: Stationary
1
In the Model Builder window, under Drucker-Prager criterion click Step 1: Stationary.
2
In the Settings window for Stationary, locate the Physics and Variables Selection section.
3
Select the Modify model configuration for study step check box.
4
In the Physics and variables selection tree, select Component 1 (comp1)>Solid Mechanics (solid)>Linear Elastic Material 1>Soil Plasticity 2.
5
Click  Disable.
Set up an auxiliary continuation sweep for the para parameter.
6
Click to expand the Study Extensions section. Select the Auxiliary sweep check box.
7
Click  Add.
8
In the table, enter the following settings:
Parameter name
Parameter value list
Parameter unit
para (Prescribed displacement)
range(0,-5e-4,-32e-3)
 
Solution 1 (sol1)
1
In the Study toolbar, click  Show Default Solver.
2
In the Model Builder window, expand the Solution 1 (sol1) node.
3
In the Model Builder window, expand the Drucker-Prager criterion>Solver Configurations>Solution 1 (sol1)>Stationary Solver 1 node, then click Parametric 1.
4
In the Settings window for Parametric, click to expand the Continuation section.
To improve convergence, set the predictor of the parametric solver to constant.
5
From the Predictor list, choose Constant.
6
In the Study toolbar, click  Compute.
Root
The second study is also parametric and solves the model assuming a Mohr-Coulomb criterion. Again, the parameter represents the vertical displacement in the center of the applied pressure (Point 7), this time running from 0 to -24.5 mm with a step size of 0.5 mm.
Add Study
1
In the Study toolbar, click  Add Study to open the Add Study window.
2
Go to the Add Study window.
3
Find the Studies subsection. In the Select Study tree, select General Studies>Stationary.
4
Click Add Study in the window toolbar.
5
In the Study toolbar, click  Add Study to close the Add Study window.
Mohr-Coulomb criterion
1
In the Model Builder window, click Study 2.
2
In the Settings window for Study, type Mohr-Coulomb criterion in the Label text field.
Step 1: Stationary
1
In the Model Builder window, under Mohr-Coulomb criterion click Step 1: Stationary.
2
In the Settings window for Stationary, locate the Physics and Variables Selection section.
3
Select the Modify model configuration for study step check box.
4
In the Physics and variables selection tree, select Component 1 (comp1)>Solid Mechanics (solid)>Linear Elastic Material 1>Soil Plasticity 1.
5
Click  Disable.
Set up an auxiliary continuation sweep for the para parameter.
6
Locate the Study Extensions section. Select the Auxiliary sweep check box.
7
Click  Add.
8
In the table, enter the following settings:
Parameter name
Parameter value list
Parameter unit
para (Prescribed displacement)
range(0,-5e-4,-24.5e-3)
 
Solution 2 (sol2)
1
In the Study toolbar, click  Show Default Solver.
To improve convergence, change the relative tolerance from 1e-3 to 1e-4 and set the predictor of the continuation solver to constant.
2
In the Model Builder window, expand the Solution 2 (sol2) node, then click Stationary Solver 1.
3
In the Settings window for Stationary Solver, locate the General section.
4
In the Relative tolerance text field, type 1e-4.
5
In the Model Builder window, expand the Mohr-Coulomb criterion>Solver Configurations>Solution 2 (sol2)>Stationary Solver 1 node, then click Parametric 1.
6
In the Settings window for Parametric, locate the Continuation section.
7
From the Predictor list, choose Constant.
8
In the Study toolbar, click  Compute.
Results
Remove the infinite element domain from the dataset for plotting.
Drucker-Prager criterion/Solution 1 (sol1)
In the Model Builder window, expand the Results>Datasets node, then click Drucker-Prager criterion/Solution 1 (sol1).
Selection
1
In the Results toolbar, click  Attributes and choose Selection.
2
In the Settings window for Selection, locate the Geometric Entity Selection section.
3
From the Geometric entity level list, choose Domain.
4
Select Domain 2 only.
Mohr-Coulomb criterion/Solution 2 (sol2)
In the Model Builder window, click Mohr-Coulomb criterion/Solution 2 (sol2).
Selection
1
In the Results toolbar, click  Attributes and choose Selection.
2
In the Settings window for Selection, locate the Geometric Entity Selection section.
3
From the Geometric entity level list, choose Domain.
4
Select Domain 2 only.
Stress, Drucker-Prager criterion
The default plots show the von Mises stress at the final step for each study and a group node containing the boundary load.
1
In the Model Builder window, under Results click Stress (solid).
2
In the Settings window for 2D Plot Group, type Stress, Drucker-Prager criterion in the Label text field.
Applied Loads, Drucker-Prager criterion
1
In the Model Builder window, under Results click Applied Loads (solid).
2
In the Settings window for Group, type Applied Loads, Drucker-Prager criterion in the Label text field.
Stress, Mohr-Coulomb criterion
1
In the Model Builder window, expand the Applied Loads, Drucker-Prager criterion node, then click Results>Stress (solid) 1.
2
In the Settings window for 2D Plot Group, type Stress, Mohr-Coulomb criterion in the Label text field.
Plastic Region, Mohr-Coulomb criterion
1
In the Model Builder window, under Results click Equivalent Plastic Strain (solid) 1.
2
In the Settings window for 2D Plot Group, type Plastic Region, Mohr-Coulomb criterion in the Label text field.
Contour 1
1
In the Model Builder window, expand the Plastic Region, Mohr-Coulomb criterion node, then click Contour 1.
2
In the Settings window for Contour, locate the Expression section.
3
In the Expression text field, type solid.epeGp>0.
Deformation 1
1
Right-click Contour 1 and choose Deformation.
2
In the Settings window for Deformation, locate the Scale section.
3
Select the Scale factor check box.
4
In the associated text field, type 10.
5
In the Plastic Region, Mohr-Coulomb criterion toolbar, click  Plot.
Applied Loads, Mohr-Coulomb criterion
1
In the Model Builder window, under Results click Applied Loads (solid) 1.
2
In the Settings window for Group, type Applied Loads, Mohr-Coulomb criterion in the Label text field.
Create a plot that displays the part of the model that undergoes plastic deformation.
Plastic Region, Drucker-Prager criterion
1
In the Model Builder window, under Results click Equivalent Plastic Strain (solid).
2
In the Settings window for 2D Plot Group, type Plastic Region, Drucker-Prager criterion in the Label text field.
Contour 1
1
In the Model Builder window, expand the Plastic Region, Drucker-Prager criterion node, then click Contour 1.
2
In the Settings window for Contour, locate the Expression section.
3
In the Expression text field, type solid.epeGp>0.
Deformation 1
1
Right-click Contour 1 and choose Deformation.
2
In the Settings window for Deformation, locate the Scale section.
3
Select the Scale factor check box.
4
In the associated text field, type 10.
5
In the Plastic Region, Drucker-Prager criterion toolbar, click  Plot.
6
Click the  Zoom Extents button in the Graphics toolbar.
Finally, follow the steps below to reproduce the graph in Figure 3.
Footing Pressure vs. Displacement
1
In the Home toolbar, click  Add Plot Group and choose 1D Plot Group.
2
In the Settings window for 1D Plot Group, type Footing Pressure vs. Displacement in the Label text field.
3
Locate the Legend section. From the Position list, choose Lower right.
Point Graph 1
1
Right-click Footing Pressure vs. Displacement and choose Point Graph.
2
In the Settings window for Point Graph, locate the Data section.
3
From the Dataset list, choose Drucker-Prager criterion/Solution 1 (sol1).
4
Select Point 7 only.
5
Locate the y-Axis Data section. In the Expression text field, type abs(footing_pressure).
6
Select the Description check box.
7
In the associated text field, type Footing pressure.
8
Locate the x-Axis Data section. From the Parameter list, choose Expression.
9
In the Expression text field, type abs(v).
10
Select the Description check box.
11
In the associated text field, type Vertical displacement.
12
Click to expand the Legends section. Select the Show legends check box.
13
From the Legends list, choose Manual.
14
In the table, enter the following settings:
Legends
Drucker_Prager
Point Graph 2
1
Right-click Point Graph 1 and choose Duplicate.
2
In the Settings window for Point Graph, locate the Data section.
3
From the Dataset list, choose Mohr-Coulomb criterion/Solution 2 (sol2).
4
Locate the Legends section. In the table, enter the following settings:
Legends
Mohr-Coulomb
Footing Pressure vs. Displacement
1
In the Model Builder window, click Footing Pressure vs. Displacement.
2
In the Footing Pressure vs. Displacement toolbar, click  Plot.
This graph shows the footing pressure as a function of the vertical displacement. As you can see, both curves reach the same failure level.