
|
|
1
|
|
2
|
In the Select Physics tree, select Electrochemistry>Corrosion, Deformed Geometry>Corrosion, Secondary.
|
|
3
|
Click Add.
|
|
4
|
Click
|
|
5
|
In the Select Study tree, select Preset Studies for Selected Physics Interfaces>Secondary Current Distribution>Time Dependent with Initialization.
|
|
6
|
Click
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
1
|
|
2
|
|
3
|
|
4
|
Click Browse.
|
|
5
|
Browse to the model’s Application Libraries folder and double-click the file localized_corrosion_microstructure.txt.
|
|
6
|
Click Import.
|
|
7
|
Find the Functions subsection. In the table, enter the following settings:
|
|
8
|
|
9
|
|
10
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
1
|
|
2
|
In the Rename 2D Plot Group dialog box, type 2D Plot Group : Cross-sectional microstructure in the New label text field.
|
|
3
|
Click OK.
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
Browse to the model’s Application Libraries folder and double-click the file localized_corrosion_parameters.txt.
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
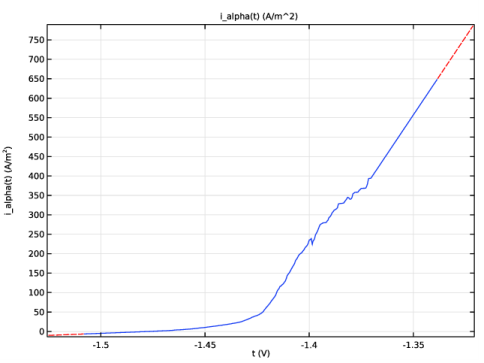
Browse to the model’s Application Libraries folder and double-click the file localized_corrosion_i_alpha.txt.
|
|
6
|
Locate the Interpolation and Extrapolation section. From the Interpolation list, choose Piecewise cubic.
|
|
7
|
|
8
|
|
9
|
|
10
|
Click
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
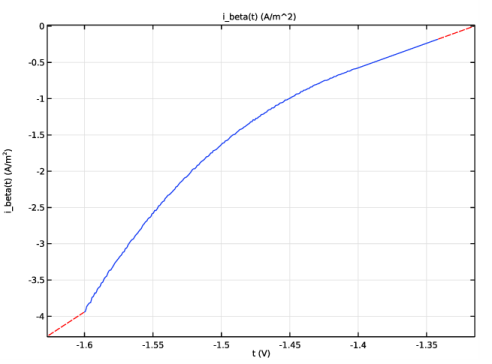
Browse to the model’s Application Libraries folder and double-click the file localized_corrosion_i_beta.txt.
|
|
6
|
Locate the Interpolation and Extrapolation section. From the Interpolation list, choose Piecewise cubic.
|
|
7
|
|
8
|
|
9
|
|
10
|
Click
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
Browse to the model’s Application Libraries folder and double-click the file localized_corrosion_variables.txt.
|
|
1
|
In the Model Builder window, under Component 1 (comp1)>Secondary Current Distribution (cd) click Electrolyte 1.
|
|
2
|
|
3
|
|
1
|
|
3
|
In the Settings window for Electrode Surface, click to expand the Dissolving-Depositing Species section.
|
|
4
|
Click
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
In the Stoichiometric coefficients for dissolving-depositing species: table, enter the following settings:
|
|
5
|
Locate the Electrode Kinetics section. From the iloc,expr list, choose User defined. In the associated text field, type (i_alpha(-phil))*(1-micro(x,y)).
|
|
1
|
|
2
|
|
3
|
From the iloc,expr list, choose User defined. In the associated text field, type (i_beta(-phil))*micro(x,y).
|
|
1
|
In the Model Builder window, under Component 1 (comp1)>Multiphysics click Nondeforming Boundary 1 (ndb1).
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
5
|
|
1
|
|
2
|
|
3
|
|
5
|
|
6
|
|
7
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
Click
|
|
7
|
|
8
|
|
9
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
In the associated text field, type Surface beta phase fraction.
|
|
1
|
|
2
|
|
4
|
|
1
|
|
2
|
In the Rename 1D Plot Group dialog box, type 1D Plot Group : Surface beta phase fraction evolution in the New label text field.
|
|
3
|
Click OK.
|
|
1
|
|
2
|
|
3
|
|
4
|
Locate the Plot Settings section. In the y-axis label text field, type Average anode current density (A/m<sup>2</sup>).
|
|
1
|
In the Model Builder window, expand the 1D Plot Group : Surface beta phase fraction evolution 1 node, then click Global 1.
|
|
2
|
|
1
|
In the Model Builder window, right-click 1D Plot Group : Surface beta phase fraction evolution 1 and choose Rename.
|
|
2
|
In the Rename 1D Plot Group dialog box, type 1D Plot Group : Average anode current density evolution in the New label text field.
|
|
3
|
Click OK.
|