
|
|
σ11 (MPa)
|
||||
|
σ22 (MPa)
|
||||
|
σ12 (MPa)
|
|
σ11 from benchmark
|
σ11, computed
|
σ22 from benchmark
|
σ22, computed
|
σ12 from benchmark
|
σ12, computed
|
|
|
•
|
Modeling a composite laminated shell requires a surface geometry (2D), in general called a base surface, and a Layered Material node which adds an extra dimension (1D) to the base surface geometry in the surface normal direction. In the Layered Material node, you can model many layers stacked on top of each other having different thickness, material properties, and fiber orientations. You can also optionally specify the interface materials between the layers and control mesh elements in each layer.
|
|
•
|
From a constitutive equations point of view, you can either use the Layerwise (LW) theory based Layered Shell interface, or the Equivalent Single Layer (ESL) theory based Layered Linear Elastic Material node in the Shell interface.
|
|
•
|
To analyze the results in a composite shell, you can either create slice plot using a Layered Material Slice plot in order to see the in-plane variation of a quantity, or you can create a Through Thickness plot to see the out-of-plane variation of a quantity. In order to visualize the results as a 3D solid object, you can use the Layered Material dataset which creates a virtual 3D solid object combining a surface geometry (2D) and the extra dimension (1D).
|
|
1
|
|
2
|
|
3
|
Click Add.
|
|
4
|
Click
|
|
5
|
|
6
|
Click
|
|
1
|
|
2
|
|
3
|
|
4
|
Browse to the model’s Application Libraries folder and double-click the file failure_prediction_in_a_laminated_composite_shell_materialproperties.txt.
|
|
1
|
|
1
|
|
2
|
|
4
|
Click Add three times.
|
|
6
|
|
7
|
Locate the Layer Definition section. Click Layer Cross Section Preview in the upper-right corner of the section.
|
|
8
|
Click to expand the Preview Plot Settings section. In the Thickness-to-width ratio text field, type 0.4.
|
|
9
|
|
10
|
Locate the Layer Definition section. Click Layer Cross Section Preview in the upper-right corner of the section.
|
|
11
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
In the Show More Options dialog box, in the tree, select the check box for the node Physics>Advanced Physics Options.
|
|
3
|
Click OK.
|
|
4
|
|
5
|
|
2
|
In the Settings window for Layered Linear Elastic Material, locate the Linear Elastic Material section.
|
|
3
|
|
1
|
|
2
|
|
1
|
|
2
|
In the Settings window for Safety, type Safety: Tsai-Wu Orthotropic Criterion in the Label text field.
|
|
3
|
|
4
|
Create six similar Safety nodes by duplicating the Safety 1 node. Replace the failure criterion according to the table below:
|
|
1
|
|
2
|
|
1
|
|
1
|
|
3
|
In the Settings window for Prescribed Displacement/Rotation, locate the Prescribed Displacement section.
|
|
4
|
|
1
|
|
3
|
|
4
|
|
5
|
|
1
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
Browse to the model’s Application Libraries folder and double-click the file failure_prediction_in_a_laminated_composite_shell_failure_indices.txt.
|
|
8
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
Browse to the model’s Application Libraries folder and double-click the file failure_prediction_in_a_laminated_composite_shell_safety_factors.txt.
|
|
8
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
Browse to the model’s Application Libraries folder and double-click the file failure_prediction_in_a_laminated_composite_shell_stresses.txt.
|
|
8
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
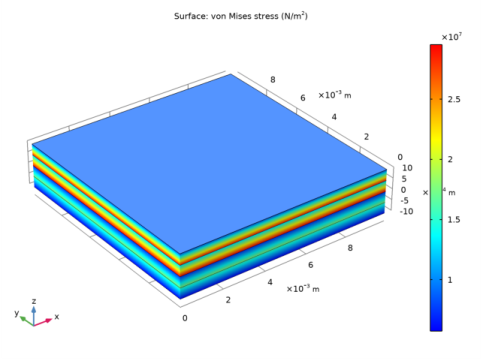
Click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1 (comp1)>Shell>Stress>shell.mises - von Mises stress - N/m².
|
|
4
|
|
5
|
|
6
|
|
7
|
|
1
|
|
2
|
|
3
|
|
5
|
|
1
|
Create three similar Layered Material Slice nodes by duplicating the node above, and replacing the local z-coordinate according to the following table. Replace the color table in the subsequent Layered Material Slice nodes, and replace the Z-component field in the corresponding Deformation node with the following choices in the table:
|
|
2
|
|
1
|
|
2
|
In the Settings window for 3D Plot Group, type Hoffman Safety Factors (Ply) in the Label text field.
|
|
3
|
|
1
|
|
2
|
|
3
|
Click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1 (comp1)>Shell>Safety>Hoffman>shell.llem1.lsf3.s_f - Hoffman safety factor.
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
Create three similar Layered Material Slice nodes by duplicating the Ply 1 node, and replace the local z-coordinate according to the following table. Replace the choice of color table in the subsequent Layered Material Slice nodes, and also replace the Z-component field in the corresponding Deformation node with the following choices in the table:
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
In the Settings window for Surface, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1 (comp1)>Shell>Stress>shell.mises - von Mises stress - N/m².
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
In the Settings window for 1D Plot Group, type von Mises Stress (Through-Thickness) in the Label text field.
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|