You are viewing the documentation for an older COMSOL version. The latest version is available here.
PDF
Tilted Pad Thrust Bearing
Introduction
Tilted pad thrust bearings are used in a variety of rotating machineries that have to withstand high thrust loading. The thrust load is transferred from a sliding part to a stationary part through hydrodynamic oil films. The tilted pad thrust bearing consists of a series of flat surfaces sliding over stationary tilted pads. The motion of the sliding flat surface drags the lubricant in toward the diminishing gap between the tilted pad and the sliding surface. The pressure developed in the lubricant between the sliding surface and the tilted pad counteracts the external load applied to the sliding surface and thus prevents contact between the two surfaces. Reynolds equation is solved on the surface of the tilted pad to find the pressure distribution on the surface of the tilted pad. This load is used in the structural analysis of the tilted pad to find its elastic deformation.
Model Definition
The pressure in the lubricant (engine oil) is governed by Reynolds equation. For an incompressible fluid with no slip condition, Reynolds equation in the continuum range is given by
In the above equation, ρ is the density (SI unit: kg/m3), h is the lubricant thickness, η  is the viscosity (SI unit: Pa.s), p is the pressure (SI unit: Pa), a is the location (SI unit: m) of the channel base, va is the tangential velocity (SI unit: m/s) of the channel base, b is the location (SI unit: m) of the solid wall, and vb is the tangential velocity (SI unit: m/s) of the solid wall. Here the sliding surface is considered the base. Because the pressure is constant through the lubricant film thickness, COMSOL uses the tangential derivative operator ∇T (that is, the projection of the gradient operator to the tangent plane) to calculate the pressure distribution on the lubricant surface. The Reynolds equation is solved on the surface of the tilted pad. The external load (Wext) applied to the sliding surface is counterbalanced by the pressure in the lubricant. This is imposed as the constraint:
(1)
The hydrodynamic pressure exerted by the lubricant causes elastic deformation of the two surfaces containing the lubricant. In this example, the surface of interest is the stationary tilted pad. The hydrodynamic pressure is used as a mechanical load on the tilted pad to calculate the elastic deformation of the pad. This example also performs a parametric study on the degree of tilt.
Figure 1 shows the lubricant thickness distribution on the surface of the tilted pad. The arrows indicate the direction of rotation of a flat surface over the tilted pad.
Figure 1: Lubricant thickness and the direction of rotation of the flat surface.
boundary conditions
Reynolds Equation
The edges of the top surface of the tilted pad are assigned a boundary condition of ambient pressure
Structural Mechanics
The top face of the tilted pad has a face load
The bottom boundary is fixed with zero displacements in the x, y, and z directions. All the other boundaries are free.
Results and discussion
The pressure distribution in the engine oil is shown in Figure 2. As one would expect, the pressure is at maximum toward the region of diminishing film height. The corresponding elastic deformation (exaggerated) and displacement of the tilted pad is shown in Figure 3.
Figure 2: Pressure distribution in engine oil.
Figure 3: Elastic deformation of the tilted pad.
Application Library path: CFD_Module/Thin-Film_Flow/tilted_pad_bearing
Modeling Instructions
From the File menu, choose New.
New
In the New window, click  Model Wizard.
Model Wizard
1
In the Model Wizard window, click  3D.
2
In the Select Physics tree, select Fluid Flow>Thin-Film Flow>Thin-Film Flow, Shell (tffs).
3
Click Add.
4
In the Select Physics tree, select Structural Mechanics>Solid Mechanics (solid).
5
Click Add.
6
Click  Study.
7
In the Select Study tree, select General Studies>Stationary.
8
Click  Done.
Global Definitions
Parameters 1
1
In the Model Builder window, under Global Definitions click Parameters 1.
2
In the Settings window for Parameters, locate the Parameters section.
3
In the table, enter the following settings:
Name
Expression
Value
Description
tilt
1e-4
1E-4
Tilt parameter
h0
10[um]
1E-5 m
Initial film thickness
W_ext
5[kN]
5000 N
External load
omega
1[rad/s]
1 rad/s
Angular velocity
Geometry 1
Work Plane 1 (wp1)
1
In the Geometry toolbar, click  Work Plane.
2
In the Settings window for Work Plane, click  Show Work Plane.
Work Plane 1 (wp1)>Plane Geometry
In the Model Builder window, click Plane Geometry.
Work Plane 1 (wp1)>Circle 1 (c1)
1
In the Work Plane toolbar, click  Circle.
2
In the Settings window for Circle, locate the Size and Shape section.
3
In the Radius text field, type 0.2.
4
In the Sector angle text field, type 45.
5
Locate the Rotation Angle section. In the Rotation text field, type -135.
6
Click to expand the Layers section. In the table, enter the following settings:
Layer name
Thickness (m)
Layer 1
0.1
7
Click  Build Selected.
8
Click the  Zoom Extents button in the Graphics toolbar.
Work Plane 1 (wp1)>Delete Entities 1 (del1)
1
Right-click Plane Geometry and choose Delete Entities.
2
In the Settings window for Delete Entities, locate the Entities or Objects to Delete section.
3
From the Geometric entity level list, choose Domain.
4
On the object c1, select Domain 1 only.
5
Click  Build Selected.
6
Click the  Zoom Extents button in the Graphics toolbar.
Extrude 1 (ext1)
1
In the Model Builder window, under Component 1 (comp1)>Geometry 1 right-click Work Plane 1 (wp1) and choose Extrude.
2
In the Settings window for Extrude, locate the Distances section.
3
In the table, enter the following settings:
Distances (m)
0.01
4
In the Geometry toolbar, click  Build All.
Form Union (fin)
1
Click  Build All.
2
Click the  Go to Default View button in the Graphics toolbar.
3
Click the  Zoom Extents button in the Graphics toolbar.
The model geometry is now complete.
Definitions
Cylindrical System 2 (sys2)
In the Definitions toolbar, click  Coordinate Systems and choose Cylindrical System.
Variables 1
1
In the Definitions toolbar, click  Local Variables.
2
In the Settings window for Variables, locate the Variables section.
3
In the table, enter the following settings:
Name
Expression
Unit
Description
U
-omega*sys2.r*sin(sys2.phi)
m/s
Slider velocity, x-component
V
omega*sys2.r*cos(sys2.phi)
m/s
Slider velocity, y-component
F_fluid
intop1(pfilm)
 
Total fluid load
Here intop1 refers to a nonlocal integration coupling for the sliding surface; define this coupling as follows.
Integration 1 (intop1)
1
In the Definitions toolbar, click  Nonlocal Couplings and choose Integration.
2
In the Settings window for Integration, locate the Source Selection section.
3
From the Geometric entity level list, choose Boundary.
4
Select Boundary 4 only.
Thin-Film Flow, Shell (tffs)
1
In the Model Builder window, under Component 1 (comp1) click Thin-Film Flow, Shell (tffs).
2
In the Settings window for Thin-Film Flow, Shell, locate the Boundary Selection section.
3
Click  Clear Selection.
4
Select Boundary 4 only.
Fluid-Film Properties 1
1
In the Model Builder window, under Component 1 (comp1)>Thin-Film Flow, Shell (tffs) click Fluid-Film Properties 1.
2
In the Settings window for Fluid-Film Properties, locate the Wall Properties section.
3
In the hw1 text field, type h0-tilt*x.
4
From the uw list, choose Displacement field (solid).
5
Locate the Base Properties section. Specify the ub vector as
0
x
0
y
Deltax_b
z
Here, Deltax_b is a constant displacement that takes a value such that the total load constraint in Equation 1 is fulfilled. You will define Deltax_b using a Global Equation feature node added to the Structural Mechanics user interface shortly.
6
From the vb list, choose User defined. Specify the vector as
U
x
V
y
0
z
Add Material
1
In the Home toolbar, click  Add Material to open the Add Material window.
2
Go to the Add Material window.
3
In the tree, select Built-in>Nylon.
4
Click Add to Component in the window toolbar.
5
In the tree, select Liquids and Gases>Liquids>Engine oil.
6
Click Add to Component in the window toolbar.
7
In the Home toolbar, click  Add Material to close the Add Material window.
Materials
Nylon (mat1)
1
In the Model Builder window, under Component 1 (comp1)>Materials click Nylon (mat1).
2
In the Settings window for Material, locate the Material Contents section.
3
In the table, enter the following settings:
Property
Variable
Value
Unit
Property group
Density
rho
0.33
kg/m³
Basic
Engine oil (mat2)
1
In the Model Builder window, click Engine oil (mat2).
2
In the Settings window for Material, locate the Geometric Entity Selection section.
3
From the Geometric entity level list, choose Boundary.
4
Select Boundary 4 only.
Solid Mechanics (solid)
In the Model Builder window, under Component 1 (comp1) click Solid Mechanics (solid).
Fixed Constraint 1
1
In the Physics toolbar, click  Boundaries and choose Fixed Constraint.
2
Select Boundary 3 only.
Boundary Load 1
1
In the Physics toolbar, click  Boundaries and choose Boundary Load.
2
Select Boundary 4 only.
3
In the Settings window for Boundary Load, locate the Force section.
4
From the FA list, choose Fluid load on wall (tffs/ffp1).
5
Click the  Show More Options button in the Model Builder toolbar.
6
In the Show More Options dialog box, in the tree, select the check box for the node Physics>Equation-Based Contributions.
7
Click OK.
Global Equations 1
1
In the Physics toolbar, click  Global and choose Global Equations.
2
In the Settings window for Global Equations, locate the Global Equations section.
3
In the table, enter the following settings:
Name
f(u,ut,utt,t) (1)
Initial value (u_0) (1)
Initial value (u_t0) (1/s)
Description
Deltax_b
F_fluid-W_ext
0
0
Channel base displacement enforcing total load constraint
4
Locate the Units section. Click  Select Dependent Variable Quantity.
5
In the Physical Quantity dialog box, type displacement in the text field.
6
Click  Filter.
7
In the tree, select General>Displacement (m).
8
Click OK.
9
In the Settings window for Global Equations, locate the Units section.
10
Click  Select Source Term Quantity.
11
In the Physical Quantity dialog box, type force in the text field.
12
Click  Filter.
13
In the tree, select General>Force (N).
14
Click OK.
Mesh 1
Mapped 1
1
In the Mesh toolbar, click  Boundary and choose Mapped.
2
Select Boundary 4 only.
Size
1
In the Model Builder window, click Size.
2
In the Settings window for Size, locate the Element Size section.
3
From the Predefined list, choose Finer.
4
Click  Build All.
Swept 1
1
In the Mesh toolbar, click  Swept.
2
In the Settings window for Swept, click  Build All.
Study 1
Step 1: Stationary
1
In the Model Builder window, under Study 1 click Step 1: Stationary.
2
In the Settings window for Stationary, locate the Physics and Variables Selection section.
3
In the table, clear the Solve for check box for Solid Mechanics (solid).
In the first step, solve only for the Lubrication Shell variables to get an initial solution for the coupled problem. Add a separate study step for the latter solution stage.
Stationary 2
1
In the Study toolbar, click  Study Steps and choose Stationary>Stationary.
2
In the Settings window for Stationary, click to expand the Study Extensions section.
3
Select the Auxiliary sweep check box.
4
Click  Add.
5
In the table, enter the following settings:
Parameter name
Parameter value list
Parameter unit
tilt (Tilt parameter)
range(1e-4,(5e-4-1e-4)/19,5e-4)
 
Solution 1 (sol1)
1
In the Study toolbar, click  Show Default Solver.
2
In the Model Builder window, expand the Solution 1 (sol1) node.
3
In the Model Builder window, click Dependent Variables 2.
4
In the Settings window for Dependent Variables, locate the Scaling section.
5
From the Method list, choose Manual.
6
In the Scale text field, type 1e-5.
7
In the Model Builder window, click Pressure (comp1.pfilm).
8
In the Settings window for Field, locate the Scaling section.
9
From the Method list, choose Initial value based.
The pressure differs in scale by about 11 orders of magnitude. It therefore needs a separate scaling factor, which you can take from the initial solution.
The default segregated solver does not work for this problem, which is better solved fully coupled.
10
In the Model Builder window, expand the Study 1>Solver Configurations>Solution 1 (sol1)>Stationary Solver 2 node.
11
Right-click Stationary Solver 2 and choose Fully Coupled.
12
In the Study toolbar, click  Compute.
Results
The first default plot group shows the fluid pressure as a surface plot for the final tilt value in the parametric sweep. Modify this plot to display the one shown in Figure 2 as follows:
Fluid Pressure (tffs)
1
In the Model Builder window, under Results click Fluid Pressure (tffs).
2
In the Settings window for 3D Plot Group, locate the Data section.
3
From the Parameter value (tilt) list, choose 1E-4.
4
Locate the Plot Settings section. Clear the Plot dataset edges check box.
Surface 1
1
In the Model Builder window, expand the Fluid Pressure (tffs) node, then click Surface 1.
2
In the Settings window for Surface, locate the Coloring and Style section.
3
From the Coloring list, choose Gradient.
4
From the Bottom color list, choose Blue.
5
Select the Reverse color gradient check box.
Surface 2
1
In the Model Builder window, right-click Fluid Pressure (tffs) and choose Surface.
2
In the Settings window for Surface, locate the Expression section.
3
In the Expression text field, type 1.
4
Locate the Coloring and Style section. From the Coloring list, choose Uniform.
5
From the Color list, choose Gray.
Selection 1
1
Right-click Surface 2 and choose Selection.
2
In the Settings window for Selection, locate the Selection section.
3
From the Selection list, choose All boundaries.
4
Select Boundaries 1–3, 5, and 6 only.
5
In the Fluid Pressure (tffs) toolbar, click  Plot.
6
Click the  Zoom Extents button in the Graphics toolbar.
The second default plot group shows a surface plot of the von Mises stress and a deformation plot of the displacement. Change this plot group to display the deformation plot in Figure 3 by following these steps:
Stress (solid)
1
In the Model Builder window, click Stress (solid).
2
In the Settings window for 3D Plot Group, click  Plot First.
Surface 1
1
In the Model Builder window, expand the Stress (solid) node, then click Surface 1.
2
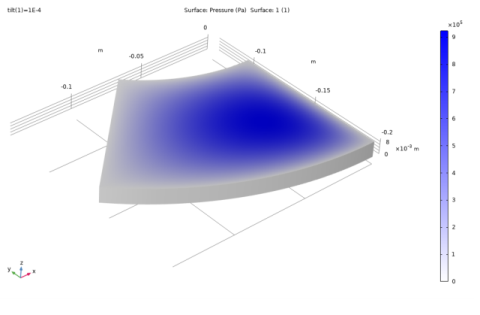
In the Settings window for Surface, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1 (comp1)>Solid Mechanics>Displacement>solid.disp - Displacement magnitude - m.
3
Locate the Expression section. In the Unit field, type um.
4
In the Stress (solid) toolbar, click  Plot.
The following steps reproduce Figure 1.
Lubricant thickness
1
In the Model Builder window, right-click Fluid Pressure (tffs) and choose Duplicate.
2
In the Settings window for 3D Plot Group, type Lubricant thickness in the Label text field.
Surface 1
1
In the Model Builder window, expand the Lubricant thickness node, then click Surface 1.
2
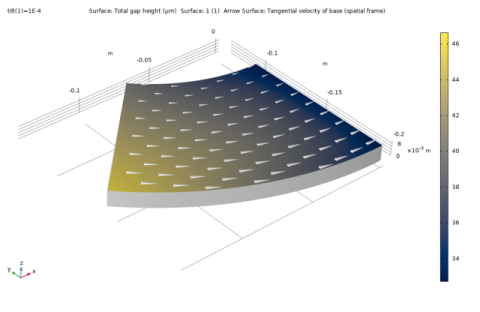
In the Settings window for Surface, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1 (comp1)>Thin-Film Flow, Shell>Wall and base properties>tffs.h - Total gap height - m.
3
Locate the Expression section. From the Unit list, choose µm.
4
In the Lubricant thickness toolbar, click  Plot.
5
Locate the Coloring and Style section. From the Coloring list, choose Color table.
6
From the Color table list, choose Cividis.
7
Clear the Reverse color table check box.
Arrow Surface 1
1
In the Model Builder window, right-click Lubricant thickness and choose Arrow Surface.
2
In the Settings window for Arrow Surface, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1 (comp1)>Thin-Film Flow, Shell>Wall and base properties>tffs.vbtx,...,tffs.vbtz - Tangential velocity of base (spatial frame).
3
Locate the Coloring and Style section. From the Arrow type list, choose Cone.
4
From the Color list, choose White.
5
In the Lubricant thickness toolbar, click  Plot.