PDF
An Equivalent Circuit Model for a Nickel-Metal Hydride Battery
Introduction
Equivalent circuits models are commonly employed for modeling electrochemical devices. This simulation approach relies on a lumped approach for representing the underlying electrochemical processes using simple electrical circuit elements, without a detailed description of the electrode materials, geometry configuration, and physical processes. The equivalent circuit models are simple and heuristic to capture voltage and current characteristics of transient or steady state data. The parameters in each circuit element are typically obtained by fitting the model to experimental data, and the individual parameter values may be difficult to correlate to specific parts of, or phenomena occurring in, the electrochemical cell.
This tutorial defines an equivalent circuit model for a nickel-metal hydride (NiMH) battery. A similar modeling approach may however also be used to model other battery chemistries.
Model Definition
The 0D model simulates a nickel-metal hydride battery using an equivalent circuit model. The model consists of two resistors, a capacitor, a current source, and a voltage source depending on the battery state-of-charge (SOC). Various charge-discharge cycles at different C-rates are simulated using a parametric sweep.
Figure 1: Equivalent Circuit diagram used for modeling the Ni-MH battery. The numbers denote the node numbers in the Battery Equivalent Circuit interface.
The circuit used in this model is based on the Newman-Ong (Ref. 1) approach to modeling electrochemical systems.
Figure 1 represents the equivalent circuit used in this simulation. The series resistance (R1) represents the ohmic resistance and the RC couple (a resistor-R2 and capacitor-C1 connected in parallel) represents the charge transfer polarization process. The time constant for the RC couple is assumed to be 15 s. The Battery Open Circuit Voltage node (OCV1) requires the battery open circuit voltage data, EOCV (V), as function of state-of-charge. Initial battery capacity and state-of-charge are also required as inputs for the Battery Open Circuit Voltage node.
The load cycle is represented through a current source (I1) connected in series with the Battery Open Circuit Voltage node.
The fundamental equations solved in the Battery Equivalent Circuit interface is Kirchhoff’s current law. A current balance for each branch node (see Figure 1) is defined as:
By summing the voltage around resistors R1 and R2, we get:
By summing the voltage around capacitor C1, we get:
The time dependent study for a charge discharge cycle for various C-rates is computed.
Results and Discussion
Figure 2 shows the computed node voltage at node 3, during charge discharge for different C-rates.
Figure 2: Voltage at node 3 for different C-rates.
Figure 3: Open circuit potential and state-of-charge for different C-rates.
Figure 3 shows the open circuit potential and state-of-charge for various C-rates. The model is able to capture the charge discharge characteristics of NiMH batteries.
Notes About the COMSOL Implementation
EOCV for the intercalation electrodes is calculated via following equation (Ref. 2):
where SOC is the state-of-charge and νj,discharge are the coefficients used to determine the open circuit cell potential. The values of the coefficients are given in Table 1.
Table 1: Parameter Describing open circuit cell potential.
Parameter
Unit
For Discharge
 νj
1
3
 U0
V
1.779
 ν1(V)
V
0.6845
 ν2(V)
V
-1.1779
 ν3(V)
V
0.6127
References
1. I.J. Ong and J. Newman, “Double Layer Capacitance in a Dual Lithium Ion Insertion Cell,” J. Electrochemical Society, vol. 146, no. 12, pp. 4360–4365, 1999.
2. M.W. Verbrugge and R.S. Conell, “Electrochemical and Thermal Characterization of Battery Design Modules Commensurate with Electric Vehicle Integration,” J. Electrochemical Society, vol. 149, no. 1, pp. A45–A53, 2002.
Application Library path: Battery_Design_Module/Batteries,_General/nimh_equivalent_circuit_battery
Modeling Instructions
This tutorial demonstrates how to build an equivalent circuit battery model and run a time-dependent simulation for a charge/discharge load cycle.
From the File menu, choose New.
New
In the New window, click  Model Wizard.
Model Wizard
1
In the Model Wizard window, click  0D.
2
In the Select Physics tree, select Electrochemistry>Batteries>Battery Equivalent Circuit (cir).
3
Click Add.
4
Click  Study.
5
In the Select Study tree, select General Studies>Time Dependent.
6
Click  Done.
Global Definitions
Parameters 1
Import the model parameters from a text file.
1
In the Model Builder window, under Global Definitions click Parameters 1.
2
In the Settings window for Parameters, locate the Parameters section.
3
Click  Load from File.
4
Browse to the model’s Application Libraries folder and double-click the file nimh_equivalent_circuit_battery_parameters.txt.
Step 1 (step1)
In the Home toolbar, click  Functions and choose Global>Step.
Definitions
Variables 1
1
In the Model Builder window, under Component 1 (comp1) right-click Definitions and choose Variables.
The battery charging and discharging variables are set up as follows:
2
In the Settings window for Variables, locate the Variables section.
3
Click  Load from File.
4
Browse to the model’s Application Libraries folder and double-click the file nimh_equivalent_circuit_battery_variables.txt.
Electrical Circuit (cir)
Set up the equivalent circuit for the battery.
Resistor 1 (R1)
1
In the Model Builder window, under Component 1 (comp1)>Electrical Circuit (cir) click Resistor 1 (R1).
2
In the Settings window for Resistor, locate the Device Parameters section.
3
In the R text field, type R1.
Battery Open Circuit Voltage 1 (OCV1)
Information about the battery characteristics is provided as an input to the Battery Open Circuit Voltage node. Next, import the open circuit potential versus state-of-charge data for nickel metal hydride (Ni-MH) battery.
1
In the Model Builder window, click Battery Open Circuit Voltage 1 (OCV1).
2
In the Settings window for Battery Open Circuit Voltage, locate the Capacity and Initial State-of-Charge section.
3
In the Qcell,0 text field, type Q0.
4
In the SOCcell,0 text field, type SOC_0.
5
Locate the Open Circuit Voltage section. Click  Clear Table.
6
Click  Load from File.
7
Browse to the model’s Application Libraries folder and double-click the file nimh_equivalent_circuit_battery_E_OCP_data.txt.
Current Source 1 (I1)
Set up the battery load.
1
In the Model Builder window, click Current Source 1 (I1).
2
In the Settings window for Current Source, locate the Device Parameters section.
3
In the isrc text field, type i_load.
Resistor-Capacitor Couple 1 (RC1)
Next, define the RC couple in the circuit to represent polarization.
1
In the Model Builder window, click Resistor-Capacitor Couple 1 (RC1).
2
In the Settings window for Resistor-Capacitor Couple, locate the Device Parameters section.
3
From the list, choose Resistance and capacitance.
4
In the R text field, type R2.
5
In the C text field, type C1.
Study 1
Set up a time-dependent study and a parametric sweep for various charge/discharge C-rates.
Parametric Sweep
1
In the Study toolbar, click  Parametric Sweep.
2
In the Settings window for Parametric Sweep, locate the Study Settings section.
3
Click  Add.
4
In the table, enter the following settings:
Parameter name
Parameter value list
Parameter unit
C_rate (C-rate)
2 4 8
1
Step 1: Time Dependent
1
In the Model Builder window, click Step 1: Time Dependent.
2
In the Settings window for Time Dependent, locate the Study Settings section.
3
In the Output times text field, type range(0,t_cycle/1000,t_cycle).
4
In the Study toolbar, click  Compute.
Results
Plot the currents, voltage, and state-of-charge resulting from the simulation.
Load Cycle Voltage
1
In the Model Builder window, expand the Results node.
2
Right-click Results and choose 1D Plot Group.
3
In the Settings window for 1D Plot Group, type Load Cycle Voltage in the Label text field.
4
Locate the Data section. From the Dataset list, choose Study 1/Parametric Solutions 1 (sol2).
Global 1
1
Right-click Load Cycle Voltage and choose Global.
2
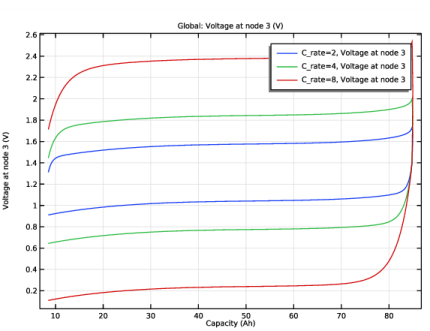
In the Settings window for Global, click Replace Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Electrical Circuit>Node voltages>cir.v_3 - Voltage at node 3 - V.
3
Locate the x-Axis Data section. From the Parameter list, choose Expression.
4
In the Expression text field, type Q0*comp1.cir.OCV1_SOC.
5
From the Unit list, choose Ah.
6
Select the Description check box.
7
In the associated text field, type Capacity.
8
In the Load Cycle Voltage toolbar, click  Plot.
9
Click the  Zoom Extents button in the Graphics toolbar.
Open Circuit Voltage and SOC vs. Time
1
In the Model Builder window, right-click Load Cycle Voltage and choose Duplicate.
2
In the Settings window for 1D Plot Group, type Open Circuit Voltage and SOC vs. Time in the Label text field.
3
Click to expand the Title section. From the Title type list, choose Label.
4
Locate the Plot Settings section. Select the Two y-axes check box.
Open Circuit Voltage
1
In the Model Builder window, expand the Open Circuit Voltage and SOC vs. Time node, then click Global 1.
2
In the Settings window for Global, click Replace Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Electrical Circuit>cir.OCV1.E_OCV - Open circuit voltage - V.
3
In the Label text field, type Open Circuit Voltage.
4
Locate the x-Axis Data section. From the Parameter list, choose Time.
5
In the Open Circuit Voltage and SOC vs. Time toolbar, click  Plot.
6
Click to expand the Coloring and Style section. Find the Line style subsection. From the Line list, choose Dashed.
Cell State-of-Charge
1
In the Model Builder window, right-click Open Circuit Voltage and SOC vs. Time and choose Global.
2
In the Settings window for Global, click Replace Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Electrical Circuit>cir.OCV1.SOC - State-of-charge.
3
In the Label text field, type Cell State-of-Charge.
4
Locate the y-Axis section. Select the Plot on secondary y-axis check box.
5
Locate the Coloring and Style section. From the Color list, choose Cycle (reset).
6
In the Open Circuit Voltage and SOC vs. Time toolbar, click  Plot.
7
Click the  Zoom Extents button in the Graphics toolbar.