
|
|
•
|
|
•
|
|
•
|
Electrolyte: 1.0 M LiPF6 in EC:DEC (1:1 by weight).
|



|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
In the Settings window for Interpolation, type Relative volume change as function of soc in the Label text field.
|
|
3
|
Locate the Definition section. In the table, enter the following settings:
|
|
4
|
|
5
|
Locate the Interpolation and Extrapolation section. From the Interpolation list, choose Piecewise cubic.
|
|
6
|
|
7
|
|
1
|
|
2
|
|
3
|
|
4
|
Browse to the model’s Application Libraries folder and double-click the file diffusion_induced_stress_variables.txt.
|
|
1
|
In the Model Builder window, expand the Porous Electrode 1 node, then click Particle Intercalation 1.
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
1
|
|
2
|
|
3
|
|
1
|
In the Model Builder window, expand the Porous Electrode 2 node, then click Porous Electrode Reaction 1.
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
In the associated text field, type Battery cell voltage (V).
|
|
6
|
|
7
|
|
1
|
|
2
|
|
3
|
|
4
|
From the Component list, choose Extra Dimension from Particle Intercalation 1 (liion_pce1_pin1_xdim).
|
|
1
|
|
2
|
In the Settings window for 1D Plot Group, type Negative particle concentration in the Label text field.
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
Locate the y-Axis Data section. In the Expression text field, type comp1.atxd1(15e-6,liion.cs_pce1/liion.csmax).
|
|
8
|
|
1
|
|
2
|
|
3
|
|
4
|
Click to expand the Coloring and Style section. Find the Line style subsection. From the Line list, choose Dashed.
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
In the associated text field, type Normalized particle dimension (1).
|
|
6
|
|
7
|
In the associated text field, type Normalized lithium concentration (1).
|
|
8
|
|
1
|
|
2
|
In the Settings window for 1D Plot Group, type Diffusion-induced stress, radial component in the Label text field.
|
|
3
|
Locate the Plot Settings section. In the y-axis label text field, type Diffusion-induced stress, radial component (Pa).
|
|
1
|
In the Model Builder window, expand the Diffusion-induced stress, radial component node, then click Line Graph 1.
|
|
2
|
|
3
|
|
4
|
Locate the y-Axis Data section. In the Expression text field, type comp1.atxd1(15e-6,liion.sr_pce1).
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|
|
9
|
|
1
|
|
2
|
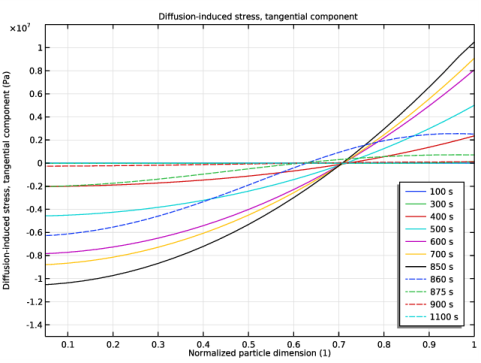
In the Settings window for 1D Plot Group, type Diffusion-induced stress, tangential component in the Label text field.
|
|
3
|
Locate the Plot Settings section. In the y-axis label text field, type Diffusion-induced stress, tangential component (Pa).
|
|
1
|
In the Model Builder window, expand the Diffusion-induced stress, tangential component node, then click Line Graph 1.
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
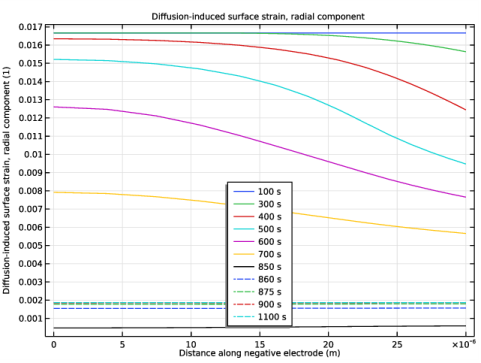
In the Settings window for 1D Plot Group, type Diffusion-induced surface strain, radial component in the Label text field.
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
7
|
Click Replace Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Lithium-Ion Battery>Stress and strain>liion.er_surface_pce1 - Diffusion-induced surface strain, radial component.
|
|
8
|
|
1
|
|
2
|
|
3
|
|
4
|
Locate the Coloring and Style section. Find the Line style subsection. From the Line list, choose Dashed.
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
In the associated text field, type Distance along negative electrode (m).
|
|
7
|
|
8
|
|
1
|
|
2
|
In the Settings window for 1D Plot Group, type Diffusion-induced surface strain, tangential component in the Label text field.
|
|
3
|
Locate the Title section. In the Title text area, type Diffusion-induced surface strain, tangential component.
|
|
1
|
In the Model Builder window, expand the Diffusion-induced surface strain, tangential component node, then click Line Graph 1.
|
|
2
|
In the Settings window for Line Graph, click Replace Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Lithium-Ion Battery>Stress and strain>liion.etheta_surface_pce1 - Diffusion-induced surface strain, tangential component.
|
|
1
|
|
2
|
In the Settings window for Line Graph, click Replace Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Lithium-Ion Battery>Stress and strain>liion.etheta_surface_pce1 - Diffusion-induced surface strain, tangential component.
|
|
1
|
|
2
|
|
1
|
|
2
|
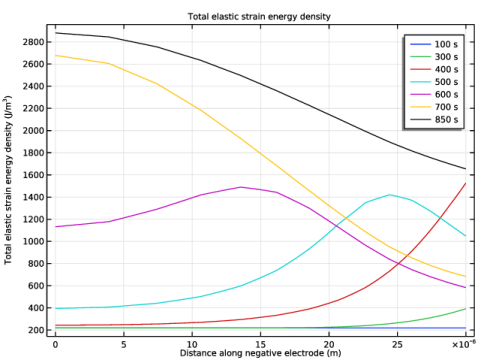
In the Settings window for 1D Plot Group, type Total elastic strain energy density in the Label text field.
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
7
|
Click Replace Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Lithium-Ion Battery>Stress and strain>liion.Ws_tot_pce1 - Total elastic strain energy density - J/m³.
|
|
8
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
In the associated text field, type Distance along negative electrode (m).
|
|
6
|
|
1
|
|
2
|
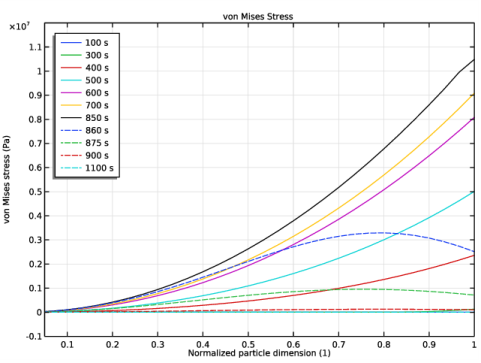
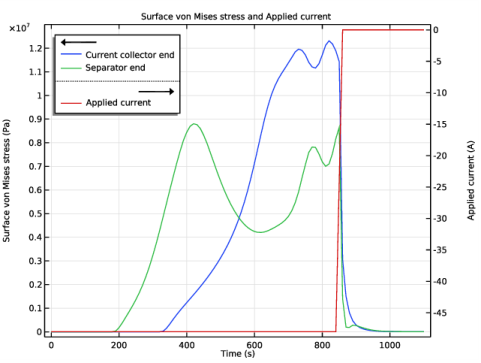
In the Settings window for 1D Plot Group, type Surface von Mises stress versus time in the Label text field.
|
|
1
|
|
3
|
In the Settings window for Point Graph, click Replace Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Lithium-Ion Battery>Stress and strain>liion.mises_surface_pce1 - Surface von Mises stress - Pa.
|
|
4
|
|
5
|
|
1
|
|
2
|
In the Settings window for Global, click Replace Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Definitions>Variables>Iapp - Applied current - A.
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|