Helmholtz Resonator Analyzed with Different Frequency Domain Solvers

This example simulates a simple three-dimensional axisymmetric Helmholtz resonator, a classic acoustics model of a resonating circuit with a known theoretical solution. The idealized version considered here consists of a tube and a closed volume in series, which are exposed to a harmonically oscillating pressure. Real-world phenomena explained by the resonator include, among others, the resonance from blowing across the top of an empty bottle and the sound produced by closed-cavity drums such as the djembe and by subwoofers. This model illustrates the use of different numerical solvers. The model shows how to solve this pressure acoustics problem for a range of frequencies using the following solvers: (a) Frequency Domain, with and without Asymptotic Waveform Evaluation (AWE) for faster solution, and (b) Frequency Domain-Modal, which reconstructs the frequency response based on a specified set of eigenmodes.

Figure 1: Illustrations of the Helmholtz resonator.

Model Definition

The model consists of a tube and volume coupled in series driven by a harmonically oscillating pressure p0( t) = p0 eiωt at the tube inlet. The Helmholtz resonator (schematically depicted in Figure 1) is one of the simplest resonating circuits. This circuit is typically described using lumped-parameter (equivalent circuit) modeling (see, for example, Ref. 1) as a serial coupling of an acoustic inertance L (equivalent to inductance in electric circuits and to mass in point-mass mechanics) caused by acceleration of the fluid in the tube and an acoustic compliance C (equivalent to capacitance in electric circuits and a spring in point-mass mechanics) arising from compression of the volume; see Figure 1 and Figure 3.

Figure 2: Diagram of the equivalent electric circuit to the Helmholtz resonator.

Because compression of the fluid volume and acceleration of the fluid in the tube are not instantaneous events but instead occur on specific time scales (each given by the geometry together with the properties of the fluid), the response of the resonator depends on the frequency, and there exists a frequency that maximizes the response — in other words, a resonance frequency ωR. This is of course to be expected given the direct analogy to electric LC circuits, and by the same analogy we find that the resonance frequency is given by

(1)

As detailed in Ref. 1, the acoustic lumped-parameter elements are given by

(2)

where ρ0 is the background quiescent density of the fluid, c0 is the background quiescent speed of sound, l is the tube length, a is the tube radius, S is the cross-sectional area of the tube transverse to the direction of the flow, γ is the end correction factor (detailed below), and V is the closed volume. Thus, using Equation 2 in Equation 1 we find that the resonance frequency ωR is given by

(3)

where in the last equation we have assumed that the volume is a sphere with

and the tube is cylindrical so S = πa2.

End correction factor γ: physical origin and approximate numerical value

When the fluid exits the tube and enters the volume, the acoustic waves disperse and the acoustic pressure drops. However, the waves initially continue along the axis of the tube when they just leave it, and moreover, they cannot move into the region occupied by the tube. Consequently, they do not completely disperse immediately as they leave the tube and the immediate region downstream of the tube is therefore still felt by the fluid in the tube where it imposes an acoustic load. In ideal models, this load results in an additional acoustic inertance corresponding to an effective increase in the length of the tube by γa. In other words, the total length of the lumped-parameter inertance L in Equation 2 is longer than the actual tube length l.

The factor γ depends on the specific geometry of the tube-volume connection and is of the order unity, Ref. 1 and 2. We shall take for reference an infinite flange for which the correction factor is γ = 0.82 (Ref. 2); this is not fully correct because the acoustic pressure disperses less in the circular geometry resulting in a larger acoustic load.

Solver descriptions

Using the default settings for the Frequency Domain solver, it solves the problem subjected to harmonic excitation at a set of specified excitation frequencies. While this can be time-consuming for larger frequency sweeps, the (numerically) exact solution is calculated explicitly at every frequency, and so the solutions from this solver can always be expected to be correct (assuming convergence of the model and appropriate meshing to resolve all length scales of the physics).

To accommodate larger sweeps, this solver also contains the option to apply asymptotic waveform evaluation (AWE). This approach does not explicitly compute the exact solution at all frequencies but instead performs a Taylor expansion of the solution about a few exact solutions and otherwise uses a lower-order approximation (Padé or Taylor) to estimate the solution across the required frequency range.

Finally, the Frequency Domain Modal solver can also be used to perform a frequency sweep. For this, it first computes a set of system eigenfrequencies and associated eigenmodes (searching either within a user-defined range, or for a user-defined number of frequencies). The full solution across the frequency sweep is then approximated by a linear combination of the basis set formed by the eigensolutions (see Notes About the COMSOL Implementation).

Goals of analysis

This pressure acoustics problem is solved in a specified frequency regime using different solvers, with the dual purpose of illustrating the capabilities of the solvers and also highlight the solver-specific settings to be aware of. The following preset solvers are used: (a) Frequency Domain, with and without Asymptotic Waveform Evaluation (AWE) for faster solution, and (b) Frequency Domain-Modal, which reconstructs the frequency response based on the eigenfrequencies in the specified range.

Resistance due to acoustic radiation

As a final note, it should be mentioned that the equivalent circuit diagram in Figure 2 is incorrect. A full equivalent circuit description of the resonator should also include the acoustic radiation resistance R caused by the dissipated energy out of the tube when the fluid in the tube moves into the volume, see Figure 3. Mathematical formulas for the resistance in a number of situations may be found in Ref. 1. However, the value of the resistance does not affect the resonance frequency (the only read-out used here), only the absolute level of the impedance of the system, so we are well-justified in ignoring R.

Figure 3: Diagram of the equivalent electric circuit to the Helmholtz resonator including the radiation resistance R.

Results and Discussion

This model uses the absolute acoustic pressure averaged over the end volume

(4)

to investigate the response. We find that the lowest eigenfrequency indeed corresponds to the resonance predicted by the lumped-parameter model, and that this theoretical prediction indeed is in good agreement with the numerical results. However, the full numerical COMSOL Multiphysics solutions illustrate the many higher modes that are ignored in the simple lumped-parameter model.

Comparing the different solvers, it is noted that they all produce the same response for the frequency sweep; see Figure 4 and Figure 5 on logarithmic and linear scales, respectively. The sound pressure level at 1043 Hz is depicted in Figure 6. The AWE and modal based frequency sweep methods are quite useful to speed up the running times of large models with a large number of frequencies requested. Due to the small number of degrees of freedom in this model, it is not possible to measure any speed-up in CPU time. See the next section for details.

Figure 4: Frequency sweep for the readout

illustrating agreement between all solvers and the theory for the first eigenfrequency and also illustrating agreement between all solvers for the higher frequencies.

Figure 5: Same frequency sweep as in Figure 4 here shown on a linear frequency scale to emphasize the higher frequencies.

Figure 6: Sound pressure level computed as a default output from the simulations, here shown for f = 1043.2 Hz.

Notes About the COMSOL Implementation

•

As a general rule of thumb, at least five quadratic elements should be used to resolve each wavelength. Therefore, the maximum mesh element size is set to 1/5 of the shortest wavelengths present, c_air/fmax.

•

The AWE option requires an expression to evaluate the solver performance (AWE expression). An integral of the absolute pressure across the entire system is used, but other functions defined on either the whole system or parts of it could be used as well.

•

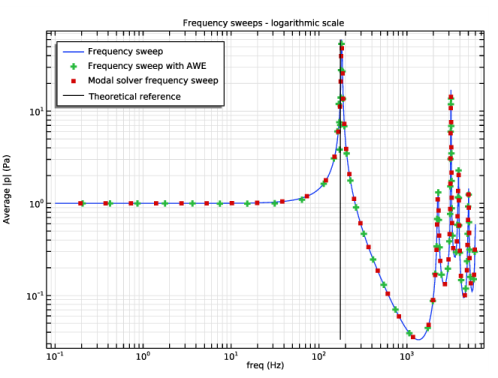
When several resonance frequencies are present, the default parameters for the AWE option may use some tuning, for example, using an adequate value (see under the node). In this model, the default value of 0.001 is used and gives reasonable results (when compared to the other methods). Lowering the value to 0.0001 will improve the high frequency results slightly (see the linear scale plot). Other settings are in general less important, like changing the number of points to linearize about (), changing the number of terms in the Taylor expansion about each point (), or changing from Padé to Taylor expansion of the approximating solution (). In the current setup we chose a relatively high upper frequency bound so about 10 resonance frequencies are present in the sweep. Had the upper frequency limit been lowered so only the first resonance was included (for instance, by setting fmax = 100 Hz), then the default relative AWE tolerance would have sufficed. Note that if either end of the frequency range is close to a resonance, the AWE solver can become unreliable.

•

The linper operator informs the solver that the term in the expression is a perturbation (a source term) that must be included in the linearized problem. The modal solver will only use the pressure under the linper operator as a source, while the other solvers will ignore this perturbation term.

•

To obtain good results with the Modal solver up to fmax, we must set the upper limit in its eigenfrequency search to 1.5*fmax to capture modes that may have an influence on the highest part of the frequency of interest. Using only fmax as the upper limit results in poorer estimates of the solution at higher frequencies.

•

The AWE option and the Frenquency Domain-Modal solver both rely on approximating the solution using a few exact solutions in the sweep range. Thus, these methods provide greater speed-up in CPU time if only few resonances fall in the sweep range, or if it is comparatively easier to find the eigensolutions relative to all the full solutions. Thus, these methods will be especially useful for large models and fine frequency sweeps over broad ranges. As an example, it is possible to update the parameter hmax to 0.5 mm to increase the size of the model. Solving the frequency sweep will take then approximately 170 s, while the AWE solver will require 55 s and the modal based frequency sweep will require only 39 s. The speed up will depend on the number of frequencies requested and the number of resonances present in the frequency of interest.

•

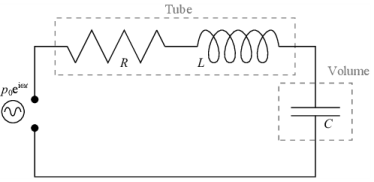
Finally, note that we define the model in terms of geometric parameters (a, L, and R). This makes it easy to quickly include parametric sweeps in the geometry, which, for instance, could be used to tune the lowest eigenfrequency.

References

1. D.T. Blackstock, Fundamentals of Physical Acoustics, John Wiley & Sons, 2000.

2. A.D. Pierce, Acoustics: An introduction to its physical principles and applications, Acoustical Society of America, 1989.

Acoustics_Module/Tutorials,_Pressure_Acoustics/helmholtz_resonator_solvers

Modeling Instructions

From the menu, choose .

New

In the window, click

Model Wizard

In the window, click

In the tree, select .

Click .

Click

In the tree, select .

Click

Global Definitions

Parameters 1

Load all model parameters from a file; these include geometrical parameters and physical properties of the air.

In the window, under click .

In the window for , locate the section.

Click

Browse to the model’s Application Libraries folder and double-click the file helmholtz_resonator_solvers_parameters.txt.

Geometry 1

Construct the simple 2D axisymmetric geometry of the resonator from Figure 1 using rectangles and circles.

Rectangle 1 (r1)

In the toolbar, click

You start by making the tube. It has length L and radius a.

In the window for , locate the section.

In the text field, type a.

In the text field, type L.

Locate the section. In the text field, type -L.

Circle 1 (c1)

In the toolbar, click

Proceed to make the volume which has radius Rv and is placed after the tube. You ensure an overlap of a/2 knowing that you will merge the tube and volume into one object (the resonator). Note that objects or parts of objects extending into the left-hand side of the symmetry line (r = 0) will be removed, so you will not have to manually remove the left half of the circle.

In the window for , locate the section.

In the text field, type Rv.

Locate the section. In the text field, type -(L+Rv-a/2).

Union 1 (uni1)

In the toolbar, click

and choose .

Clean up the remaining parts of the geometry.

Click in the window and then press Ctrl+A to select both objects.

Delete Entities 1 (del1)

In the window, right-click and choose .

On the object , select Boundaries 1, 2, and 5 only.

In the window for , click

Click the

button in the toolbar.

In the toolbar, click

Materials

Now add the material. For this simple model it suffices to use tabulated values for the physical parameters of air, which can be defined manually by adding a blank material and assign to it the values rho_air and c_air. Alternatively load air from the Material Library.

My air

In the window, under right-click and choose .

In the window for , type My air in the text field.

Locate the section. In the table, enter the following settings:


Property	Variable	Value	Unit	Property group
Density	rho	rho_air	kg/m³	Basic
Speed of sound	c	c_air	m/s	Basic

Next define integrated variables and an integration operation. First define an integration coupling that integrates over the volume V which will be used for evaluating the system response intop1. Then define the average absolute pressure in the volume which will be used as a readout of the system response.

Definitions

Integration 1 (intop1)

In the toolbar, click

and choose .

Select Domain 1 only.

Variables 1

In the window, right-click and choose .

In the window for , locate the section.

Click

Browse to the model’s Application Libraries folder and double-click the file helmholtz_resonator_solvers_variables.txt.

Pressure Acoustics, Frequency Domain (acpr)

Pressure Acoustics 1

Next, you define that you will be solving Pressure Acoustics in the entire domain, and you apply the boundary conditions.

Click the

button in the toolbar.

Pressure 1

In the window, right-click and choose .

Select Boundary 3 only.

The applied pressure is a combination of an constant part and a linper operator. The constant part will be used in the Frequency Domain steps and inactive in the rest, while the linper part will be active when running the Frequency Domain, Modal Step and inactive in the rest, as described in Notes About the COMSOL Implementation.

In the window for , locate the section.

In the p0 text field, type 1+linper(1).

Mesh 1

Next, define the mesh to have a maximum size corresponding to one fifth of the smallest wavelength in the system (see Notes About the COMSOL Implementation).

Free Triangular 1

In the toolbar, click