
|
|
1
|
|
2
|
|
3
|
Click Add.
|
|
4
|
Click
|
|
5
|
|
6
|
Click
|
|
1
|
|
2
|
|
3
|
|
4
|
Browse to the model’s Application Libraries folder and double-click the file ground_motion_seismic_event_parameters.txt.
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
Locate the Definition section. In the Expression text field, type 1e9*(2*(pi*f0*(t - t0))^2 - 1)*exp(-(pi*f0*(t - t0))^2).
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|
|
1
|
|
2
|
|
3
|
|
4
|
In the associated text field, type FFT of the signal (Pa).
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
1
|
|
2
|
Select the object r2 only.
|
|
3
|
|
4
|
|
5
|
Select the object pc1 only.
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
On the object par1, select Domain 1 only.
|
|
5
|
|
1
|
|
2
|
On the object fin, select Domains 4 and 5 only.
|
|
3
|
|
1
|
|
1
|
In the Model Builder window, under Component 1 (comp1) right-click Materials and choose Blank Material.
|
|
2
|
|
1
|
In the Model Builder window, under Component 1 (comp1)>Elastic Waves, Time Explicit (elte) click Elastic Waves, Time Explicit Model 1.
|
|
2
|
In the Settings window for Elastic Waves, Time Explicit Model, locate the Linear Elastic Material section.
|
|
3
|
|
1
|
|
2
|
|
1
|
|
3
|
|
4
|
|
1
|
|
1
|
|
2
|
|
3
|
Click the Custom button.
|
|
4
|
Locate the Element Size Parameters section. In the Maximum element size text field, type cr/(2*f0)/1.5.
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
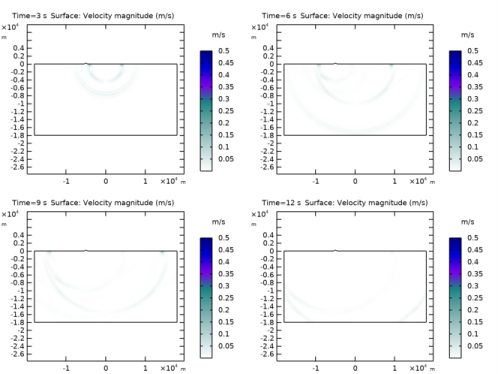
In the Model Builder window, expand the Results>Pressure and Shear Waves node, then click Surface 1.
|
|
2
|
|
3
|
|
4
|
|
5
|
Select the Description check box.
|
|
6
|
In the associated text field, type Signed squared root of the second principal invariant.
|
|
7
|
|
8
|
|
9
|
|
10
|
|
11
|