
|

|
18 μm
|
||
|
54 μm
|
||
|
7 μm
|
||
|
1
|
|
2
|
In the Select Physics tree, select Acoustics>Thermoviscous Acoustics>Thermoviscous Acoustics, Frequency Domain (ta).
|
|
3
|
Click Add.
|
|
4
|
|
5
|
Click Add.
|
|
6
|
|
7
|
Click Add.
|
|
8
|
In the Select Physics tree, select Mathematics>PDE Interfaces>Lower Dimensions>Weak Form Boundary PDE (wb).
|
|
9
|
Click Add twice.
|
|
10
|
Click
|
|
11
|
In the Select Study tree, select Preset Studies for Selected Physics Interfaces>Electrostatics>Small-Signal Analysis, Frequency Domain.
|
|
12
|
Click
|
|
1
|
|
2
|
|
3
|
|
4
|
Browse to the model’s Application Libraries folder and double-click the file condenser_microphone_lumped_parameters.txt.
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
1
|
|
2
|
|
3
|
|
4
|
Browse to the model’s Application Libraries folder and double-click the file condenser_microphone_lumped_variables.txt.
|
|
1
|
|
2
|
|
3
|
|
5
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
1
|
|
1
|
|
3
|
In the Settings window for Prescribed Mesh Displacement, locate the Prescribed Mesh Displacement section.
|
|
4
|
Specify the dx vector as
|
|
1
|
|
1
|
In the Model Builder window, under Component 1 (comp1)>Thermoviscous Acoustics, Frequency Domain (ta) click Thermoviscous Acoustics Model 1.
|
|
2
|
|
3
|
|
4
|
|
1
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|
In the Show More Options dialog box, in the tree, select the check box for the node Physics>Advanced Physics Options.
|
|
9
|
Click OK.
|
|
10
|
|
11
|
|
1
|
|
2
|
|
3
|
|
1
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
4
|
|
1
|
|
2
|
|
4
|
|
1
|
|
2
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
In the Dependent variables table, enter the following settings:
|
|
7
|
|
8
|
|
9
|
Click
|
|
10
|
|
11
|
Click OK.
|
|
1
|
In the Model Builder window, under Component 1 (comp1)>Weak Form Boundary PDE (wb) click Weak Form PDE 1.
|
|
2
|
|
3
|
|
1
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
In the Dependent variables table, enter the following settings:
|
|
7
|
|
8
|
|
9
|
Click
|
|
10
|
|
11
|
Click OK.
|
|
1
|
In the Model Builder window, under Component 1 (comp1)>Weak Form Boundary PDE 2 (wb2) click Weak Form PDE 1.
|
|
2
|
|
3
|
In the weak text field, type r*((Tm*kmsq*um-ta.iomega*(Fes+pin-p))*test(um)-Tm*dtang(um,r)*test(dtang(um,r))).
|
|
1
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
In the tree, select Built-in>Air.
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
Click in the Graphics window and then press Ctrl+A to select both domains.
|
|
5
|
|
1
|
|
3
|
|
4
|
|
1
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
1
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
1
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
1
|
|
2
|
|
3
|
In the table, clear the Solve for check boxes for Thermoviscous Acoustics, Frequency Domain (ta), Electrical Circuit (cir), and Weak Form Boundary PDE 2 (wb2).
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
Locate the Physics and Variables Selection section. In the table, clear the Solve for check boxes for Electrostatics (es) and Weak Form Boundary PDE (wb).
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
1
|
|
2
|
In the Settings window for Surface, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1 (comp1)>Thermoviscous Acoustics, Frequency Domain>Acceleration and velocity>ta.v_inst - Instantaneous local velocity - m/s.
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
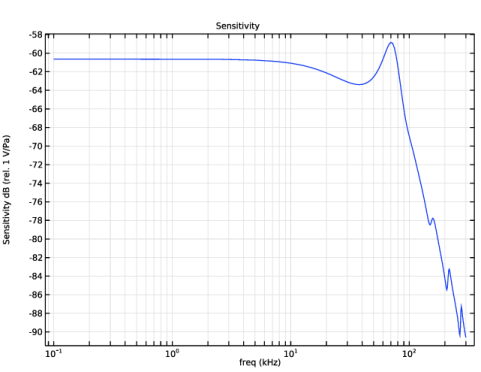
In the associated text field, type log<sub>10</sub>(|um<sub>av</sub>| (m/s)).
|
|
6
|
|
1
|
|
2
|
|
4
|
|
5
|
|
1
|
|
2
|
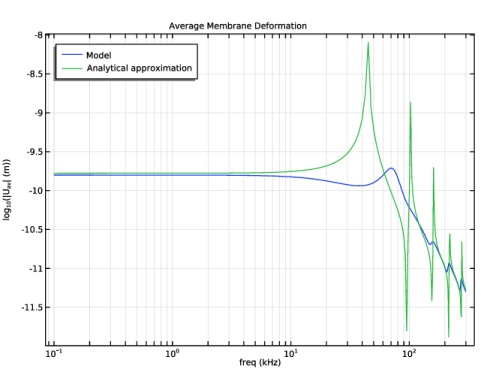
In the Settings window for 1D Plot Group, type Average Membrane Deformation in the Label text field.
|
|
3
|
|
4
|
|
5
|
In the associated text field, type log<sub>10</sub>(|U<sub>av</sub>| (m)).
|
|
6
|
|
1
|
|
2
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|