PDF
Submarine Cable 4 — Inductive Effects
Introduction
Results from the Capacitive Effects and Bonding Capacitive tutorials (the previous tutorials in this series) show there is only a weak coupling between the inductive and capacitive phenomena in the cable. In addition to this, research [1, 2] suggests 2D and 2.5D inductive models are able to provide a good approximation of the cable’s lumped quantities, and at only a fraction of the computational cost (as compared to long 3D twist models).
This justifies a 2D/2.5D inductive model that includes out-of-plane currents only. The model demonstrates methods suitable to approximate the armor twist, as well as certain milliken conductor designs. It serves as a basis and a reference for the Thermal Effects and the Inductive Effects 3D tutorials (chapters 6 and 8). Verification is included; the results are compared to the cable’s official specifications.
Model Definition
The geometry is the same as the one used in the Capacitive Effects tutorial; see Figure 1. It describes a detailed cross section (as built in the Introduction tutorial). A large number of material properties is included for the metals, the polymers, and the sea bed.
Figure 1: The cable’s cross section, including the three phases (yellow), screens (red), the XLPE (white), the armor (blue), and the fiber (green).
Theoretical Basis
The model solves Maxwell–Ampère's law in the frequency domain, and in 2D, using the out-of-plane magnetic vector potential A as a dependent variable. The underlying theory is discussed using the differential form, together with the SI unit system.
When solving, all four Maxwell’s equations are either directly or indirectly involved, together with two field definitions (E and B in terms of A) and three constitutive relations — the ones containing the material properties ε, σ, and μ:
 
 
 
 
 
Gauss’s Law:
 
Faraday’s Law:
Magnetic Gauss’s Law:
 
Maxwell–Ampère's Law:
 
 
 
 
 
Electric Field:
 
Dielectric Properties:
 
 
 
Conductive Properties:
Magnetic Flux Density:
 
Magnetic Properties:
 
 
 
 
 
 
 
 
 
 
Conservation of Current
Let us start with the notion that when current is not conserved, you get a build-up of charge. This is given by in the time domain, and in the frequency domain. You can combine this with Gauss’s law; , to get a modified current conservation law:
(1)
For the time domain, this would be , or, when using the electric field:
(2)
where the first constitutive relation; is used.
What this result shows is that a time-varying electric (displacement) field is just another kind of current density, the displacement current density. This seems reasonable. After all, if you picture a charging capacitor, you will see currents flowing from the terminals to the capacitor plates but not from one plate to the other (due to the insulating dielectric). If you stick to the conviction that current is conserved at all times, and in all places, the increasing electric field between the plates must therefore be some other kind of current.
You might have noticed this in the Capacitive Effects tutorial, where both the displacement and the conduction current density are plotted: In the insulators, the displacement current density is prominent; in the conductors, the conduction current density is prominent; and the sum of both is conserved at all times. This is why some textbooks include the displacement current in the definition of the current density:
(3)
where the second constitutive relation; is used. This relation suggests ωε is some sort of imaginary “conductivity” — one that does not involve losses (in the time domain, this is less obvious). It also explains why some people tend to use a complex permittivity in order to model resistive effects in the frequency domain.
Maxwell–Ampère's Law
The second part of our derivation starts with Maxwell–Ampère's law; , which basically states there is a direct relation between the magnetic field H that encircles a conductor and the current density that runs through it1 — in fact, the very definition of the Ampère is based on this. If you take the divergence of that, it results in something very convenient:
(4)
This is true by definition: From basic vector calculus follows that the divergence of the curl of any vector field must always be zero. In other words, if you define the current density to be equal to the curl of H, you get a current conservation law for free — there is no additional equation required to enforce this.
Gauss’s law and Maxwell–Ampère’s law have now been applied. If you add the third constitutive relation2; , you end up with the following:
(5)
 
The Magnetic Vector Potential
Now consider a vector field A, the magnetic vector potential in Vs/m (or Wb/m), whose curl is chosen to be equal to the magnetic flux density B. That is; . The magnetic vector potential is not a directly measurable field or anything, nor is it unique. Without any additional constraints there are many different fields A that fulfill the requirement3 .
A similar thing happens for the electric scalar potential V. Even for electrostatic conditions, there is no such thing as an absolute (unique) electric potential: The potential is always measured with respect to some arbitrary reference (ground). What matters is the potential difference, or the potential gradient. The same goes for the magnetic vector potential. Using this relation between A and B, and taking the divergence once again, you get:
(6)
So if you define B in terms of A; , you get magnetic flux conservation (Gauss’s law for magnetism) for free. This is for the exact same reason that you got current conservation for free.
Faraday’s Law and the Final Partial Differential Equation
If you now substitute this definition of B in Maxwell–Faraday’s equation of electromagnetic induction; , you get:
(7)
This gives you the last piece of the puzzle4: . Now, both B and E can be expressed in terms of A. If you substitute this result in Equation 5, you will find:
(8)
Finally, if you swap about some terms and put everything on the left-hand side, you get the following 2D partial differential equation for the dependent variable A:
(9)
Due to the double curl, this is known as a curl-curl-type equation. The Magnetic Fields interface uses this equation in the domains to determine the value of A, and consequently, the value of all the fields derived from it: E, D, J, B, and H.
Notice that the direction of A is the same as the direction of E (and , assuming isotropic material properties). If only the out-of-plane component of the magnetic vector potential is included (setting the other components equal to zero), in-plane currents and electric fields are neglected — considering the results seen in this tutorial series so far, this seems justified. Consequently, the 2D model treated here only produces in-plane magnetic fields. Omitting the in-plane components of A significantly simplifies and stabilizes the problem.
For the outer boundaries the default condition is used, that constrains A in the direction of the surface normal. Therefore, B will be perpendicular to the surface normal; the magnetic flux lines will flow along the surface. This is known as a magnetic insulation condition (in analogy to electric or thermal insulation). Since the surface normal of a boundary in a 2D model is in-plane, and since the magnetic vector potential is chosen to be out-of-plane only, in effect the value of A is zero on all outer boundaries. This gives you a complete set of equations and therefore a unique solution.
In order to excite the system, either an external electric field Eext or an external current density Jext is applied in the cable’s main conductors. This field comes from an outside source not included in the model, presumably a power plant or a wind farm.
Modeling Approach
The tutorial starts with the basics; by exciting a current in the phases (using a Coil feature). As a result, strong eddy currents start to flow in both the screens and the armor. This configuration is effectively the same as solid bonding5.
In an attempt to mimic the effects caused by the armor twist, the armor wires are electrically connected in series by means of a Coil group. In a third step, the coil features used to excite the phase currents, are set to Homogenized multiturn. This allows for investigating the case where the current in the central conductors is evenly distributed — due to the use of twisted, insulated strands (or milliken conductors).
The inductance per phase in mH/km is compared to the cable’s official specifications. For the AC resistance per phase, in mΩ/km, the DC resistance is used as a frame of reference:
(10)
where σcu and A refer to the copper conductivity and the total effective cross-sectional surface area of a phase respectively. The DC resistance serves as a lower bound for the AC resistance, that is; with . It represents a condition where all losses due to parasitic inductive effects have been successfully eliminated.
On Armor Twist and 2.5D
The 2D model represents a plain extrusion. In practice the armor is twisted however, with a different pitch than the central conductors have (see the Inductive Effects 3D tutorial).
As a result, every armor wire will sense every side of the cable at some point along its length (cyclic even). The first armor wire shown in the cross section (Figure 1) will be the second one a bit farther down the cable; they are indistinguishable. Therefore, all wires will have to carry the same total longitudinal current. The effect can be mimicked by putting the armor wires in series, giving you what is known as a 2.5D model [1, 2].
Note that the length of the cable cannot be used as an argument to expect variations in current here, as the cable is much shorter than the relevant wavelength:
(11)
where L and C refer to the cable’s inductance and capacitance per unit length. This wavelength is about 2.5 · 103 km, while the cable is assumed to be 10 km.
On Coil Domains
The Coil feature plays a central role in this model. It is one of the most important features included in the Magnetic Fields interface (or the AC/DC Module for that matter). The feature can be used as an active or passive element; it allows you to excite the system and to determine lumped parameters like inductance or resistance. Furthermore, it allows you to connect active or passive elements in your model to one another, to an external circuit, or to other models6. The feature supports two common conductor models: Single conductor and Homogenized multiturn.
Single Conductor Model
In case of the single conductor model, the domain behaves like a single (solid) conductor; currents are free to flow as dictated by Maxwell–Ampère’s law. Excitation is done by means of an external electric field Eext. This external electric field is then combined with the induced electric field to form a total electric field, and the total electric field is used to drive the currents. When the conductor is large enough with respect to the skin depth, skin- and proximity effects will occur. This is natural behavior.
The skin- and proximity effects will redistribute the cross-sectional current density; the current accumulates at the surface. This current accumulation leads to an increase in losses — after all, part of the conductor is not optimally used. This is why, in practice, most coils use insulated wires (turns) that are electrically thin (thin with respect to the skin depth). To be able to carry enough current, the amount of turns is increased (as opposed to increasing the thickness of the turns). This leads to the term multiturn. Moreover, the turns are placed in series7, so each turn will carry the same amount of current. With the turns being too thin to be electrically visible, a seemingly homogeneous current density distribution is achieved in a predefined direction (the direction of the wire bundle).
Homogenized Multiturn Model
With the homogenized multiturn setting, the coil domain models a bundle of turns (multiturn coil) or strands (Litz wire), as an effective material with strongly anisotropic electrical properties and a homogenized current density distribution: No current will flow unless the coil is connected to something, or short circuited. The obvious advantage of this approach, is that the individual wires do not have to be resolved by the geometry or the mesh. In both cases (single conductor and homogenized multiturn), lumped parameters are determined by integrating current densities and electric fields in the proper directions. The resulting currents and voltages are compared to derive properties like impedance, inductance, resistance, and more.
Coil Groups
The Coil group option is specifically for 2D. When enabled, the coil feature considers every connected cluster of domains in the feature selection a different instance of the same entity crossing the 2D plane multiple times. Say that you have two separate circles in your 2D model. If you add both to the selection of your coil domain with the coil group setting enabled, what you are modeling is the same coil that passes your 2D plane twice. A typical example is a 2D axisymmetric model with a number of circles representing different turns of the same helix as it revolves around its axis a number of times.
From an electrical viewpoint, this means the selected domains are connected in series. More advanced functionality is available in order to create combinations of parallel and series connections, and to reverse the current in certain domains (for more details, check the AC/DC module users guide).
Results and Discussion
Initially, the cable is modeled as a plain extrusion (a plain 2D model). The currents in the armor are oscillating way above and below the zero point, with a magnitude that differs between armor wires; see Figure 2. The armor losses are rather high: 7.6 kW/km.
The screen currents are not restricted either (due to the use of solid bonding8). The resulting loss is 13 kW/km for the three screens combined. The phase losses settle at 47 kW/km, and the AC resistance is 53 mΩ/km.
Figure 2: The real part of the out-of-plane current density distribution for the plain 2D configuration at phase . The animated version is available as reference [4].
When the armor twist is applied (in the 2.5D model), the armor currents are suppressed; see Figure 3. The armor losses go down (significantly; to 360 W/km), but at the same time, the inductance goes up; see Table 1. The reasoning behind this is as follows: For the plain 2D model, the parasitic armor currents were able to produce their own magnetic fields, opposing the ones coming from the phases (as dictated by Lenz’s law). Now that this effect is suppressed, the reluctance of the magnetic circuit has decreased. In effect, the ring of highly permeable armor wires starts to be have more like a magnetic core.
This “magnetic core” causes the overall magnetic energy in the system to go up (and along with it; the inductance). Due to this waterbed effect the phase and screen losses go up, by about 170 W and 2.1 kW per kilometer respectively. The total losses go down however, by about 7%. This is reflected by a reduced AC resistance of 49 mΩ/km.
Figure 3: The real part of the out-of-plane current density distribution for the 2.5D configuration at phase . The animated version is available as reference [6].
When compared to 3D twist models, it turns out neither the 2D nor the 2.5D model gives a perfect description. The 2D configuration is more accurate when it comes to the total losses and the resistance, while the 2.5D model is more accurate when it comes to the inductive properties — see the Inductive Effects 3D tutorial (and reference [1]).
Table 1: Results from the different twist configurations compared.
 
Plain 2D Model
2.5D Model
2.5D + Milliken
Phase Losses (kW/km)
47
47
43
Screen Losses (kW/km)
13
15
16
Armor Losses (kW/km)
7.6
0.36
0.37
Phase AC Resistance (mΩ/km)
53
49
46
Rac/Rdc Ratio ( - )
1.57
1.45
1.37
Phase Inductance (mH/km)
0.42
0.44
0.44
As a proof of concept, a means to model milliken conductors is explored. As long as the coil domains representing the phases are set to Single conductor, there is a skin effect and a proximity effect with a stronger current density near the cable’s center; see Figure 4.
Figure 4: The current density norm (phase independent), with Single conductor setting used in the phases.
When the phases are set to Homogenized multiturn, however, their current density distribution is homogenized (see section On Coil Domains). As a result, the phase losses go down significantly, to 43 kW/km. With the parasitic currents removed from the main conductors, the overall magnetic energy in the system rises again and the screens and armor are subjected to stronger fields. The screen and armor losses go up, an settle at 16 kW/km and 370 W/km, respectively.
The 2.5D+milliken configuration gives a value of 46 mΩ/km for the AC resistance. The DC resistance (as given by Equation 10) evaluates to 34 mΩ/km. Note that the DC resistance serves as a lower bound; all attempts to suppress parasitic effects (to get the losses down), resulted in the AC resistance approaching the DC one. This is reflected by the AC/DC resistance ratio9 η, going down from 1.57, to 1.45, to 1.37.
Finally, when comparing the model to the 3D twist model from the Inductive Effects 3D tutorial (and the cable’s specifications), the inductance gives a good match: 0.44 mH/km.
On Accuracy
These results look very promising. Do not forget, however, that the 2D twist variants treated here, are all approximations. To start with, losses due to in-plane eddies have been neglected altogether. In a perfectly straight cable these would be zero, but real cables are twisted. To complicate matters further, the double twist allows the magnetic armor to provide an additional low-reluctance path for the field lines — one that 2D models cannot capture. For more on this, see the Inductive Effects 3D tutorial (chapter 8).
Secondly, the homogenized current distribution in the milliken conductor should be taken with a grain of salt. Putting insulation between the strands makes them thinner, twisting them makes them longer: inductive losses may go down, but the DC resistance will go up. The used material will typically be somewhere in-between a solid conductor and a perfectly stranded, twisted one. In practice you can assume the phases to behave like solid conductors, unless you have a good reason to believe otherwise (also considering the manufacturing costs). Lastly, in this tutorial thermal effects have not yet been considered. This topic will be treated in the Thermal Effects tutorial.
References
1. J.C. del-Pino-López, M. Hatlo, and P. Cruz-Romero, “On Simplified 3D Finite Element Simulations of Three-Core Armored Power Cables,” Energies 2018, 11, 3081.
2. J.J. Bremnes, G. Evenset, R. Stølan, “Power Loss and Inductance of Steel Armoured Multi-Core Cables: Comparison of IEC Values with 2.5D FEA Results and Measurements,” (Cigré 2010).
3. Video file submarine_cable_z_animation_04_plain_2d_model,
available for download at https://www.comsol.com/model/43431.
4. Video file submarine_cable_z_animation_05_plain_2d_model_b,
available for download at https://www.comsol.com/model/43431.
5. Video file submarine_cable_z_animation_06_2.5d_model,
available for download at https://www.comsol.com/model/43431.
6. Video file submarine_cable_z_animation_07_2.5d_model_b,
available for download at https://www.comsol.com/model/43431.
Application Library path: ACDC_Module/Tutorials,_Cables/submarine_cable_04_inductive_effects
Modeling Instructions
This tutorial will focus on inductive effects. The instructions on the following pages will help you to build, configure, solve and analyze the model. If anything seems out of order, please retrace your steps. The finalized model — available in the model’s Application Libraries folder — can help you out. You can compare it directly to your current model by means of the Compare option on the Developer toolbar.
Root
The geometry, materials, and mesh have been prepared in the Introduction tutorial (chapter 1). They have been saved in the file submarine_cable_01_introduction.mph. You can start by opening this file and saving it under a new name.
Hint; if you are new to COMSOL Multiphysics, it is worthwhile to check out the Introduction tutorial first.
1
From the File menu, choose Open.
2
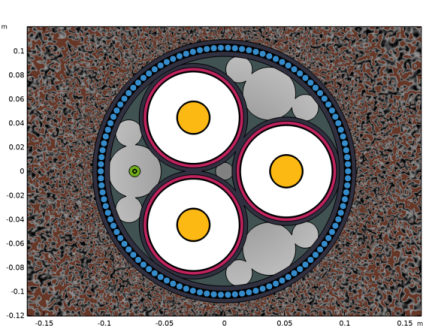
Browse to the model’s Application Libraries folder and double-click the file submarine_cable_01_introduction.mph.
3
From the File menu, choose Save As.
4
Browse to a suitable folder and type the filename submarine_cable_04_inductive_effects.mph.
Global Definitions
Some parameters have been prepared for running the model, and verifying results afterward. You can load them from a file.
Electromagnetic Parameters
1
In the Home toolbar, click  Parameters and choose Add>Parameters.
2
In the Settings window for Parameters, type Electromagnetic Parameters in the Label text field.
3
Locate the Parameters section. Click  Load from File.
4
Browse to the model’s Application Libraries folder and double-click the file submarine_cable_c_elec_parameters.txt.
The added parameters are the same as the ones used in the Capacitive Effects tutorial. f0, w0, V0 and I0 are pretty straightforward, where 1/sqrt(3) and sqrt(2) convert from phase-to-phase to phase-to-ground, and from root mean square (RMS) to peak value respectively. Scup to Dsarm are some material properties and the skin depths derived from those, and Rcon, Rpbs are analytically determined DC resistances per phase. They are given by Equation 10, and its screen equivalent.
The AC resistance will have to be determined by solving the model. Due to eddy currents, the AC resistance will be higher than the DC one (the DC resistance serves as a lower bound). Consequently, the ratio between the two, η, shows how successful losses due to parasitic inductive effects have been eliminated.
The last three; Exlpe, Cpha, and Icpha, are related to capacitive effects. They have been investigated and discussed by the previous tutorials in this series. Now that the parameters are in place, proceed by adding some physics and a frequency domain study.
Add Physics
1
In the Home toolbar, click  Add Physics to open the Add Physics window.
2
Go to the Add Physics window.
3
In the tree, select AC/DC>Electromagnetic Fields>Magnetic Fields (mf).
4
Click Add to Component 1 in the window toolbar.
5
In the Home toolbar, click  Add Physics to close the Add Physics window.
Magnetic Fields (mf)
1
In the Settings window for Magnetic Fields, locate the Domain Selection section.
2
From the Selection list, choose Electromagnetic Domains.
3
Click the  Zoom to Selection button in the Graphics toolbar.
Add Study
1
In the Home toolbar, click  Add Study to open the Add Study window.
2
Go to the Add Study window.
3
Find the Studies subsection. In the Select Study tree, select General Studies>Frequency Domain.
4
Right-click and choose Add Study.
5
In the Home toolbar, click  Add Study to close the Add Study window.
Study 1
Step 1: Frequency Domain
1
In the Settings window for Frequency Domain, locate the Study Settings section.
2
In the Frequencies text field, type f0.
A minor modification to the solver configuration is done, so that the results are more compatible with those from the Thermal Effects tutorial — it will allow for comparing figures in the same table side-by-side.
Solution 1 (sol1)
1
In the Study toolbar, click  Show Default Solver.
2
In the Model Builder window, expand the Study 1>Solver Configurations>Solution 1 (sol1)>Stationary Solver 1 node.
3
Right-click Study 1>Solver Configurations>Solution 1 (sol1)>Stationary Solver 1>Parametric 1 and choose Delete.
With the Parametric node included, the study will perform a frequency sweep containing one frequency only; f0. Without it, the study will just compute a single solution, without sweep. The difference is subtle, but will affect the way results are stored in post processing.
Materials
Now, you will see that COMSOL starts detecting missing material properties. The properties that should be added are listed in the following table. Please check all of them for the correct value, even the ones that are already filled in. A quick option is to copy-paste the values directly from this *.pdf file to COMSOL.
1
In the Model Builder window, under Component 1 (comp1)>Materials, check the following properties:
 
Label
mur
sigma [S/m]
epsilonr
mat6
Cross-linked polyethylene (XLPE)
1
1e-18[S/m]
Exlpe
mat11
Copper
Mcup
Ncon*Scup
1
mat12
Lead
Mpbs
Spbs
1
mat13
Galvanized steel
Marm
Sarm
1
Note that in the end, many material properties will be either ignored, overridden or proven to be insignificant. This is similar to what happens in the Capacitive Effects tutorial — although here, it is the conductors that will prevail (not the insulators).
Furthermore, for the copper in the central conductors the parameter Ncon is used (the conductor packing density). Ncon is the ratio between the conductor’s true cross sectional surface area Acon, and the cross section used in the geometry; pi*(Dcon/2)^2. This ratio is below unity since these conductors are not actually solid but consist of a group of compacted strands, with some insulation or gaps in-between.
Instead of modeling the strands individually, we choose to have an effective material to represent both the copper and the gaps, having a conductivity of “Ncon times the conductivity of copper”. Note that this reasoning does not apply to coil domains using the Homogenized multiturn setting, as those have their own settings for the conductivity and the cross-sectional surface area. We will get back to that later.
Modeling Instructions — Solid Bonding (Plain 2D Model)
Magnetic Fields (mf)
Now that the materials have been set and double-checked, let us have a look at the physics. With the default settings applied (out-of-plane vector potential only) the Magnetic Fields interface assumes zero in-plane currents (see section Theoretical Basis). When considering the charging currents, this assumption is justified (as seen in the Capacitive Effects tutorial). In-plane eddy currents are larger however — as seen in the Inductive Effects 3D tutorial — but still small enough to make this model a good approximation.
Start by applying currents to the three phases using a coil feature and compute your first solution (for more information on coil features, see the section On Coil Domains). To get a better view, zoom in a couple of times.
Click the  Zoom In button in the Graphics toolbar, twice.
Phase 1
1
In the Model Builder window, under Component 1 (comp1) right-click Magnetic Fields (mf) and choose the domain setting Coil.
2
In the Settings window for Coil, type Phase 1 in the Label text field.
3
Locate the Domain Selection section. From the Selection list, choose Phase 1.
The settings window for the coil feature contains a lot of sections. For many of these, the default settings are sufficient. Collapse them to have a closer look at the important part; the Coil section.
4
Click to collapse the Material Type section, the Coordinate System Selection section, and the Constitutive Relation sections.
Next, proceed by setting the currents.
5
Locate the Coil section. In the Icoil text field, type I0.
Phase 2
1
In the Physics toolbar, click  Domains and choose Coil.
2
In the Settings window for Coil, type Phase 2 in the Label text field.
3
Locate the Domain Selection section. From the Selection list, choose Phase 2.
4
Locate the Coil section. In the Icoil text field, type I0*exp(-120[deg]*j).
Phase 3
1
In the Physics toolbar, click  Domains and choose Coil.
2
In the Settings window for Coil, type Phase 3 in the Label text field.
3
Locate the Domain Selection section. From the Selection list, choose Phase 3.
4
Locate the Coil section. In the Icoil text field, type I0*exp(+120[deg]*j).
Note that, since we are in the frequency domain, expressions like exp(-120[deg]*j) or exp(-j*2*pi/3) may be used to set a 120° phase shift between the AC currents on the three main conductors.
So now you have added an Ampère’s law feature with out-of-plane vector potential (the default), some material properties and a form of excitation. Together with the frequency domain study — with the frequency set — you should be free to go. Disable the default plots and click compute.
Study 1
1
In the Model Builder window, click Study 1.
2
In the Settings window for Study, locate the Study Settings section.
3
Clear the Generate default plots check box.
4
In the Home toolbar, click  Compute.
Results
Magnetic Flux Density Norm (mf)
1
In the Home toolbar, click  Add Plot Group and choose 2D Plot Group.
2
In the Settings window for 2D Plot Group, type Magnetic Flux Density Norm (mf) in the Label text field.
Surface 1
1
Right-click Magnetic Flux Density Norm (mf) and choose Surface.
2
In the Settings window for Surface, locate the Coloring and Style section.
3
From the Color table list, choose RainbowLight.
4
In the Magnetic Flux Density Norm (mf) toolbar, click  Plot.
The first thing to notice is that the Magnetic Flux Density Norm plot is zoomed-in quite a bit. This is because it is still locked to the camera settings used in the geometry and the mesh. Let us increase the resolution and give it separate view settings.
5
Click to expand the Quality section. From the Resolution list, choose Fine.
Magnetic Flux Density Norm (mf)
1
In the Model Builder window, click Magnetic Flux Density Norm (mf).
2
In the Settings window for 2D Plot Group, locate the Plot Settings section.
3
From the View list, choose New view.
4
In the Magnetic Flux Density Norm (mf) toolbar, click  Plot.
5
Click the  Zoom Extents button in the Graphics toolbar.
6
Click the  Zoom In button in the Graphics toolbar, twice.
This plot shows the norm of the magnetic flux density. Since we are in the frequency domain, the magnetic flux density is a complex vector field. The corresponding norm is defined as  || B ||  =√ (B·B*) = (|Bx|2 + |By|2)1/2. Consequently, the plot looks three-fold symmetric and is phase independent.
Now, let us have a look at the current density norm.
Out of Plane Current Density (mf)
1
Right-click Magnetic Flux Density Norm (mf) and choose Duplicate.
2
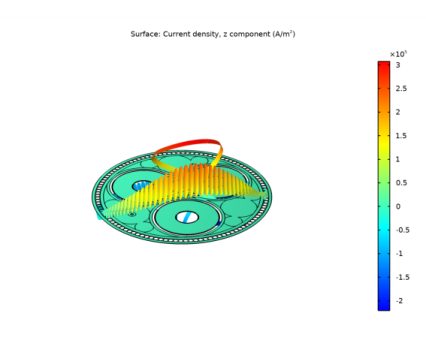
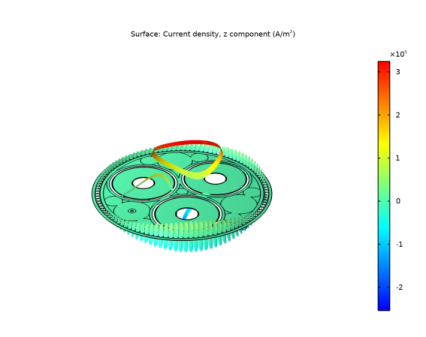
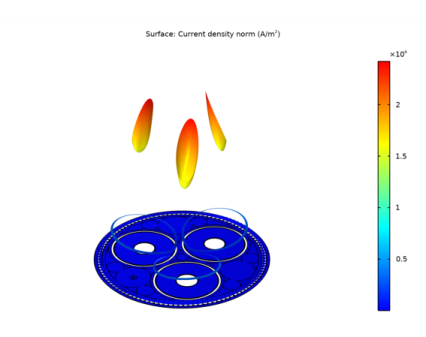
In the Settings window for 2D Plot Group, type Out of Plane Current Density (mf) in the Label text field.
3
Locate the Plot Settings section. From the View list, choose New view.
This new view is needed, as we want to decouple the camera settings of this plot from the previous one (we will get back to this).
Surface 1
1
In the Model Builder window, expand the Out of Plane Current Density (mf) node, then click Surface 1.
2
In the Settings window for Surface, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1 (comp1)>Magnetic Fields>Currents and charge>mf.normJ - Current density norm - A/m², (or just type mf.normJ in the Expression field).
3
In the Out of Plane Current Density (mf) toolbar, click  Plot.
4
Click the  Zoom Extents button in the Graphics toolbar.
5
Click the  Zoom In button in the Graphics toolbar, twice.
Here, you have switched from the variable mf.normB, to mf.normJ. For many quantities, predefined variables are available. You can find them using the buttons in the top-right corner of the Expression section, just above the text input field for the expression. There is some autocompletion functionality too (try pressing Ctrl+Space with the text input field in focus).
The current in the main conductors dominates. This current is desired (apart from the skin- and proximity effect). The parasitic currents in the screens and armor however, are not desired. Let us have a closer look at them by excluding the main conductors from the plot.
Study 1/Solution 1 (2) (sol1)
1
In the Model Builder window, expand the Results>Datasets node.
2
Right-click Results>Datasets>Study 1/Solution 1 (sol1) and choose Duplicate.
Selection
1
In the Results toolbar, click  Attributes and choose Selection.
2
In the Settings window for Selection, locate the Geometric Entity Selection section.
3
From the Geometric entity level list, choose Domain.
4
From the Selection list, choose Cable Domains.
5
Clear the selection for Phase 1, Phase 2, and Phase 3 in the Graphics window.
6
Click the  Zoom to Selection button in the Graphics toolbar.
Out of Plane Current Density (mf)
1
In the Model Builder window, click Out of Plane Current Density (mf).
2
In the Settings window for 2D Plot Group, locate the Data section.
3
From the Dataset list, choose Study 1/Solution 1 (2) (sol1).
4
In the Out of Plane Current Density (mf) toolbar, click  Plot.
5
Click the  Zoom Extents button in the Graphics toolbar.
These are the screen and armor currents. The corresponding losses are of the resistive type (as opposed to magnetic or dielectric hysteresis losses). This kind of loss, also known as Ohmic heating or Joule heating, follows from Ohm’s law. In the frequency domain, it is given by |I|2R/2, or, in differential form: |J|2/(2σ), where σ is assumed to be a scalar quantity.
Notice that, as the sea bed surrounding the cable has been excluded from the solution, the size of the plotted cross section has become smaller. Consequently, this plot has a zoom setting that differs from the first one. It is for this reason, that we preferred to have separate camera settings for this plot. Proceed by investigating the corresponding losses.
Volumetric Loss Density (mf)
1
Right-click Out of Plane Current Density (mf) and choose Duplicate.
2
In the Settings window for 2D Plot Group, type Volumetric Loss Density (mf) in the Label text field.
Surface 1
1
In the Model Builder window, expand the Volumetric Loss Density (mf) node, then click Surface 1.
2
In the Settings window for Surface, locate the Expression section.
3
In the Expression text field, type mf.Qrh.
4
Locate the Coloring and Style section. From the Color table list, choose HeatCameraLight.
5
In the Volumetric Loss Density (mf) toolbar, click  Plot.
6
Click the  Zoom Extents button in the Graphics toolbar.
The plain 2D model gives a fair approximation of the cable’s resistive losses. Note that because of its complex permeability, the armor generates magnetic hysteresis losses too; those can be evaluated using the expression “mf.Qml”. The total losses are given by mf.Qh, which is the sum of both.
The magnitude and distribution of the losses will be off though, since the model does not include the cable’s twist. Several techniques are available to mimic a twist in 2D. Before implementing some of these however, let us investigate the phase dependency of the fields and currents by creating some nice animations.
Magnetic Flux Density Norm (mf)
For this, we make the Magnetic Flux Density Norm plot phase dependent using the norm of the instantaneous vector  || Re(B) ||  = (Re(Bx)2 + Re(By)2)1/2. As opposed to the norm used previously, this one is phase dependent: As Bx and By rotate in the complex plane, Re(Bx) and Re(By) will oscillate. A contour plot of Az is added for the corresponding field lines.
Surface 1
1
In the Model Builder window, click Surface 1.
2
In the Settings window for Surface, locate the Expression section.
3
In the Expression text field, type sqrt(real(mf.Bx)^2+real(mf.By)^2).
4
Select the Description check box.
5
In the associated text field, type Magnetic flux density norm (instantaneous).
6
Locate the Coloring and Style section. From the Color table list, choose Rainbow.
7
Select the Reverse color table check box.
Contour 1
1
In the Model Builder window, right-click Magnetic Flux Density Norm (mf) and choose Contour.
2
In the Settings window for Contour, locate the Expression section.
3
In the Expression text field, type Az.
4
Click to expand the Title section. From the Title type list, choose None.
5
Locate the Coloring and Style section. From the Coloring list, choose Uniform.
6
From the Color list, choose Black.
7
Clear the Color legend check box.
8
Click to expand the Quality section. From the Resolution list, choose Fine.
9
In the Magnetic Flux Density Norm (mf) toolbar, click  Plot.
Animation 1
1
In the Results toolbar, click  Animation and choose Player.
2
In the Settings window for Animation, locate the Animation Editing section.
3
From the Sequence type list, choose Dynamic data extension.
4
Locate the Frames section. In the Number of frames text field, type 60.
5
Locate the Playing section. From the Repeat list, choose Forever.
6
Right-click Animation 1 and choose Play (see the animation from reference [3]).
Hint; if you feel generating the animation takes too long on your machine, change the quality/resolution setting of the corresponding surface and contour plot from fine, to coarse.
Creating field lines by means of a contour plot of Az is valid in this case, because of the relation B =∇× A, combined with the fact that A is strictly out of plane here. As opposed to the standard general-purpose streamline plots — the ones used for heat flux or fluid flow, for example — this contour plot gives you a physically accurate depiction of the magnetic flux lines. That is; the plot shows perfectly closed loops and the contour density is directly proportional to the instantaneous magnetic flux density. In case of streamlines it is only the direction that has meaning; the density should be taken with a grain of salt.
Furthermore, note that the act of plotting itself, takes the real part of Az only. This is because plotting an actual complex 2D scalar field would require a 3D plot. In a way, that is what the animation does; it uses time as a third dimension to show the phase information contained in the solution.
7
Click the Stop button in the Graphics toolbar.
Out of Plane Current Density (mf)
As for the shape of the field lines, you might have noticed they bend when crossing the screen and the armor. This is an additional hint that the parasitic currents are significant. Let us see how the currents behave as a function of phase.
Surface 1
1
In the Model Builder window, click Surface 1.
2
In the Settings window for Surface, locate the Expression section.
3
In the Expression text field, type mf.Jz.
(As opposed to mf.normJ, this one is phase dependent).
Height Expression 1
1
Right-click Surface 1 and choose Height Expression.
2
In the Out of Plane Current Density (mf) toolbar, click  Plot.
3
Click the  Go to Default View button in the Graphics toolbar.
Animation 2
1
In the Results toolbar, click  Animation and choose Player.
2
In the Settings window for Animation, locate the Scene section.
3
From the Subject list, choose Out of Plane Current Density (mf).
4
Locate the Animation Editing section. From the Sequence type list, choose Dynamic data extension.
5
Locate the Frames section. In the Number of frames text field, type 60.
6
Locate the Playing section. From the Repeat list, choose Forever.
7
Right-click Animation 2 and choose Play (see the animation from reference [4]).
So the currents in the armor are oscillating way above and below the zero point, with a magnitude that differs between armor wires. In practice the armor is twisted however, with a different pitch than the central conductors have. As a result all wires will carry the same total longitudinal current. The effect can be mimicked by putting the armor wires in series (giving you a 2.5D model, see section On Armor Twist and 2.5D).
Note that by using cross bonding (or single-point bonding), a similar effect can be achieved for the screens. This will be further investigated in the Bonding Inductive tutorial. In the next part we will limit ourselves to the armor twist however, as cross bonding and single-point bonding are rarely used for submarine applications.
But first, let us quantify the total losses so we can make a good comparison later on.
8
Click the Stop button in the Graphics toolbar.
Phase Losses
1
In the Results toolbar, click  More Derived Values and choose Integration>Surface Integration.
2
In the Settings window for Surface Integration, type Phase Losses in the Label text field.
3
Locate the Selection section. From the Selection list, choose Phases.
4
Locate the Expressions section. In the table, enter the following settings:
Expression
Unit
Description
mf.Qh
W/km
Phase losses (plain 2D model)
5
Click  Evaluate.
Screen Losses
1
In the Results toolbar, click  More Derived Values and choose Integration>Surface Integration.
2
In the Settings window for Surface Integration, type Screen Losses in the Label text field.
3
Locate the Selection section. From the Selection list, choose Screens.
4
Locate the Expressions section. In the table, enter the following settings:
Expression
Unit
Description
mf.Qh
W/km
Screen losses (plain 2D model)
5
Click  Evaluate.
Armor Losses
1
In the Results toolbar, click  More Derived Values and choose Integration>Surface Integration.
2
In the Settings window for Surface Integration, type Armor Losses in the Label text field.
3
Locate the Selection section. From the Selection list, choose Cable Armor.
4
Locate the Expressions section. In the table, enter the following settings:
Expression
Unit
Description
mf.Qh
W/km
Armor losses (plain 2D model)
5
Click  Evaluate.
Table
1
Go to the Table window.
The total losses per kilometer (both resistive and magnetic) should be about 47 kW, 13 kW, and 7.6 kW for the phases, screens, and armor respectively.
Furthermore, let us have a look at the lumped parameters. This is particularly useful when comparing these results with the ones from the Thermal Effects or the Inductive Effects 3D tutorial — or the cable’s official specifications and IEC 60287, for that matter.
Results
Phase AC Resistance
1
In the Results toolbar, click  Global Evaluation.
2
In the Settings window for Global Evaluation, type Phase AC Resistance in the Label text field.
3
Locate the Expressions section. In the table, enter the following settings:
Expression
Unit
Description
(mf.RCoil_1/1[m]+mf.RCoil_2/1[m]+mf.RCoil_3/1[m])/3
mohm/km
Phase AC resistance (plain 2D model)
4
Click  Evaluate.
Phase Inductance
1
In the Results toolbar, click  Global Evaluation.
2
In the Settings window for Global Evaluation, type Phase Inductance in the Label text field.
3
Locate the Expressions section. In the table, enter the following settings:
Expression
Unit
Description
(mf.LCoil_1/1[m]+mf.LCoil_2/1[m]+mf.LCoil_3/1[m])/3
mH/km
Phase inductance (plain 2D model)
4
Click  Evaluate.
Table
1
Go to the Table window.
The phase AC resistance per kilometer for the plain 2D model should be about 53 mΩ. The inductance per kilometer should be about 0.42 mH. These figures will be affected when switching to a 2.5D model. Some of them will become “more accurate” when compared to a full 3D twist model (or an actual measurement), some of them will be less accurate.
Neither the 2D nor the 2.5D model gives a perfect description. The 2D model should be more accurate when it comes to the total loss and the resistance, while the 2.5D model should be more accurate when it comes to the inductive properties — see the Inductive Effects 3D tutorial (and reference [1]).
Modeling Instructions — Armor Twist (2.5D Model)
Magnetic Fields (mf)
Proceed by applying a coil group to model the effect of the armor twist.
Cable Armor
1
In the Physics toolbar, click  Domains and choose Coil.
2
In the Settings window for Coil, type Cable Armor in the Label text field.
3
Locate the Domain Selection section. From the Selection list, choose Cable Armor.
4
Locate the Coil section. Select the Coil group check box.
5
From the Coil excitation list, choose Voltage.
6
In the Vcoil text field, type 0[V].
With the Coil group setting enabled, COMSOL considers the selected domains different instances of the same entity crossing the 2D plane multiple times. As a consequence, it puts the domains electrically in series (see section On Coil Domains). Additionally, you have set the excitation voltage to 0[V], effectively cross-circuiting the coil group. Now, the currents may flow freely as long as the total current is the same in all selected domains.
Hint; you can investigate the resulting behavior further by de-balancing the cable.
Let us compute.
Study 1
In the Home toolbar, click  Compute.
Results
Magnetic Flux Density Norm (mf)
1
In the Magnetic Flux Density Norm (mf) toolbar, click  Plot.
Notice how the field lines pass the armor more easily this time, and how the magnetic flux density distribution in the armor is more homogeneous now (for the corresponding animation, see reference [5]).
Out of Plane Current Density (mf)
1
In the Model Builder window, click Out of Plane Current Density (mf).
2
In the Out of Plane Current Density (mf) toolbar, click  Plot.
3
Click the  Go to Default View button in the Graphics toolbar.
Animation 2
1
In the Model Builder window, right-click Animation 2 and choose Play (see the animation from reference [6]).
The currents in the armor have been reduced significantly. Although they still oscillate locally inside the wire, the total net longitudinal current per armor wire is now zero (since this is a well-balanced cable). For those interested in different bonding types; feel free to investigate what happens when you add an additional coil group to the screens.
Since the coil group puts the domains in series (as opposed to forcing the total net current per domain to zero directly), the armor will show natural behavior in the sense that the losses will increase when the cable becomes de-balanced, feel free to check this.
Now, let us see how the armor twist affects the losses, the resistance, and the inductance.
2
Click the Stop button in the Graphics toolbar.
Phase Losses
1
In the Model Builder window, click Phase Losses.
2
In the Settings window for Surface Integration, locate the Expressions section.
3
In the table, update the description. Type Phase losses (2.5D model), that is; replace “plain 2D” with “2.5D”.
4
In the Settings window for Surface Integration, click Evaluate.
Screen Losses, Armor Losses, Phase AC Resistance, and Phase Inductance
Repeat these steps for Screen Losses, Armor Losses, Phase AC Resistance, and Phase Inductance.
Table
1
Go to the Table window.
The losses per kilometer should be about 47 kW, 15 kW, and 360 W for the phases, screens, and armor. As a response to the large reduction in losses for the armor, the phase- and screen losses went up (by about 170 W and 2.1 kW respectively). This waterbed effect is related to a redistribution of the magnetic energy.
The total loss in the cross section has been reduced by about 7%. This is reflected by a reduced AC resistance: 49 mΩ. The inductance increases slightly, to 0.44 mH, and by doing so, moves closer to the value given by the 3D model.
So the 2.5D model suggests the armor twist leads to an overall reduction in loss — although this should be taken with a grain of salt as some phenomena are not properly accounted for (as seen in the Inductive Effects 3D tutorial). In essence, the armor is forced to behave like some kind of Litz wire. Going further down this road, we can still gain another 3.5 kW per kilometer by modifying the main conductors.
Selection
1
In the Model Builder window, click Selection.
2
In the Settings window for Selection, locate the Geometric Entity Selection section.
3
From the Selection list, choose Cable Domains.
4
Click the  Zoom to Selection button in the Graphics toolbar.
Surface 1
1
In the Model Builder window, click Surface 1.
2
In the Settings window for Surface, locate the Expression section.
3
In the Expression text field, type mf.normJ.
4
In the Out of Plane Current Density (mf) toolbar, click  Plot.
5
Click the  Go to Default View button in the Graphics toolbar.
As you can see, the current in the main conductors is not homogeneous. There is a skin- and proximity effect, with a stronger current density near the cable’s center. We have modeled solid conductors here (apart from the correction term; Ncon).
In practice however, the main conductors consist of twisted strands. Depending on the kind of insulation (if any) between the strands, the current density may be partially homogenized. For the sake of argument, let us assume this twisting technique works perfectly — admittedly, not a realistic assumption for this particular kind of cable, but a useful exercise nonetheless.
Modeling Instructions — Phase Twist (2.5D + Milliken)
Magnetic Fields (mf)
Phase 1
1
In the Model Builder window, under Component 1 (comp1)>Magnetic Fields (mf) click Phase 1.
2
In the Settings window for Coil, locate the Coil section.
3
From the Conductor model list, choose Homogenized multiturn.
4
Locate the Homogenized Multiturn Conductor section. In the N text field, type 1.
5
In the σcoil text field, type Scup.
6
In the acoil text field, type Acon.
Phase 2, Phase 3
Repeat these steps for Phase 2, and Phase 3.
You have used the Homogenized multiturn setting here. This is ideal for coils with multiple thin turns — or Litz wires with strands much thinner than the skin depth (this includes certain milliken conductor designs). With this setting enabled, the turn or strand bundle will behave like a strongly anisotropic continuum with a homogenized cross-sectional current density distribution (see section On Coil Domains).
Since the strands are electrically connected in parallel, we set the number of turns to 1, and the wire cross section to Acon (the sum of all strands). Proceed by computing the final result.
Study 1
In the Home toolbar, click  Compute.
Results
Out of Plane Current Density (mf)
1
In the Model Builder window, under Results click Out of Plane Current Density (mf).
2
In the Out of Plane Current Density (mf) toolbar, click  Plot.
3
Click the  Go to Default View button in the Graphics toolbar.
The current distribution is homogeneous now, with the total net current going through the main conductors still the same (I0 for each phase).
Phase Losses
1
In the Model Builder window, click Phase Losses.
2
In the Settings window for Surface Integration, locate the Expressions section.
3
In the table, update the description. Type Phase losses (2.5D+milliken), that is; replace “2.5D model” with “2.5D+milliken”.
4
In the Settings window for Surface Integration, click Evaluate.
Screen Losses, Armor Losses
Repeat these steps for Screen Losses and Armor Losses.
Table
1
Go to the Table window.
The losses per kilometer should be about 43 kW, 16 kW, and 370 W for the phases, screens, and armor respectively.
Phase AC Resistance
1
In the Model Builder window, click Phase AC Resistance.
2
In the Settings window for Global Evaluation, locate the Expressions section.
3
In the table, enter the following settings:
Expression
Unit
Description
(mf.RCoil_1/1[m]+mf.RCoil_2/1[m]+mf.RCoil_3/1[m])/3
mohm/km
Phase AC resistance (2.5D+milliken)
Rcon
mohm/km
Main conductor DC resistance per phase, at 20°C (analytic)
4
Click  Evaluate.
5
Go to the Table window.
The phase resistance per kilometer should be about 46 mΩ and 34 mΩ for the AC- and DC resistance respectively. Notice that the AC resistance has moved fairly close to the DC one. As mentioned when introducing the parameters at the beginning of this tutorial, the DC resistance serves as a lower bound; all attempts done to get the losses down, resulted in the AC resistance approaching the DC one, feel free to verify this.
Phase Inductance
1
In the Model Builder window, click Phase Inductance.
2
In the Settings window for Global Evaluation, locate the Expressions section.
3
In the table, update the description. Type Phase inductance (2.5D+milliken), that is; replace “2.5D model” with “2.5D+milliken”.
4
In the Settings window for Global Evaluation, click  Evaluate.
5
Go to the Table window.
The inductance per kilometer should be about 0.44 mH. This is close to the official specifications and the 3D models, so this configuration seems to give a pretty accurate insight in the cable’s inductive performance.
Although these results look very promising, there are a couple of loose ends, still. The homogenized current in the central conductors is one of many possible approximations, and so is the solid conductor with conductivity Ncon*Scup (see section On Accuracy). Some might point out the current in the fiber’s armor should be put to zero, although the corresponding losses are negligible. Furthermore, we have the charging currents flowing through the screens, resulting in some additional losses (about 0.38 kW per phase, as determined in the Bonding Capacitive tutorial).
More significant however, is the effect of heat. Thermal effects give rise to an increased resistivity and consequently, increased losses. The cable you have modeled here is 20°C, whereas any real cable would operate at a temperature of about 80 to 90°C. The sixth tutorial in this series will include a detailed thermal analysis.
You have now completed this tutorial, subsequent tutorials will refer to the resulting file as submarine_cable_04_inductive_effects.mph. The next tutorial in this series will investigate bonding types from an inductive viewpoint.
From the File menu, choose Save.
 
1
Notice that initially, James Clerk Maxwell did not include the displacement currents, leading to a law that is valid under stationary conditions only (known as Ampère’s circuital law). He added the displacement currents a couple of years later — at equation (112) in his 1861 paper “On Physical Lines of Force” — resulting in what is now referred to as “Maxwell–Ampère’s law” (or, less formally; “Ampère’s law”).

2
Since this model runs in the frequency domain, you are restricted to linear material properties. It is possible to approximate the effect of a nonlinear material though; using effective nonlinear magnetic curves. For more on this, check the AC/DC Module User’s Guide.

3
This phenomenon leads to gauge freedom. For more info, see the AC/DC Module User’s Guide.

4
Notice that, with the electric field being defined solely in terms of the magnetic vector potential, we have been excluding the electric scalar potential, that is; V = 0. This choice is known as the Weyl or Hamiltonian gauge. For more information about different gauges and gauge fixing, see the AC/DC Module User’s Guide.

5
For more information on bonding types, see the Bonding Capacitive and Bonding Inductive tutorials.

6
This is demonstrated in the Bonding Inductive tutorial.

7
Note that Litz wires form an exception. In case of a Litz wire, the different strands (or turns) are placed in parallel instead of series. A similar current for each strand is achieved by twisting the strands in such a fashion that each individual strand occupies every part of the total cross section at some point along the wire.

8
For more information on bonding types, see the Bonding Capacitive and Bonding Inductive tutorials.

9
Together with the analytically determined DC resistance, this ratio is used in the Thermal Effects tutorial to provide an approximate value for the AC resistance.