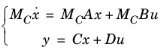mphstate

Get state-space matrices for a dynamic system.

str = mphstate(model,soltag,'Out',{'SP'})

str = mphstate(model,soltag,'Out',{'SP1','SP2',...})

str = mphstate(model,soltag,'out',{'SP'}) returns a MATLAB® structure str containing the state-space matrix SP assembled using the solver node soltag and accessible as str.SP, SP being taken from the Out property list.

str = mphstate(model,soltag,'out',{'SP1','SP2',...}) returns a MATLAB structure str containing the state-space matrices SP1, SP2, ... assembled using the solver node soltag and accessible as str.SP1and str.SP2. SP1 and SP2 being taken from the out property list.

The function mphstate accepts the following property/value pairs:

Table 6-39: property value for the mphstate command
property	value	default	description
out	MA \| MB \| A \| B \| C \| D \| Mc \| Null \| ud \| x0		Output matrix
keepfeature	off \| on	off	Keep the StateSpace feature in the model
input	String		Input variables
output	String		Output variables
sparse	off \| on	off	Return sparse matrices
initmethod	init \| sol	init	Use linearization point
initsol	soltag \| zero	soltag	Solution to use for linearization
solnum	Positive integer	auto	Solution number

The property Sparse controls whether the matrices A, B, C, D, M, MA, MB, and Null are stored in the sparse format.

The equations correspond to the system below:

where x are the state variables, u are the input variables, and y are the output variables.

A static linearized model of the system can be described by:

The full solution vector U can be then obtained from

where Null is the null-space matrix, ud the constraint contribution, and u0 is the linearization point, which is the solution stored in the sequence once the state-space export feature is run.

The matrices MC and MCA are produced by the same algorithms that do the finite-element assembly and constraint elimination in COMSOL Multiphysics. MC and MCA are the same as the matrices DC (eliminated mass matrix) and −KC (KC is the eliminated stiffness matrix). The matrices are produced from an exact residual vector Jacobian calculation (that is, differentiation of the residual vector with respect to the degrees of freedoms x) plus an algebraic elimination of the constraints. The matrix C is produced in a similar way (that is, the exact output vector Jacobian matrix plus constraint elimination).

The matrices MCB and D are produced by a numerical differentiation of the residual and output vectors, respectively, with respect to the input parameters (the algorithm systematically perturbs the input parameters by multiplying them by a factor 1+10−8).

The input cannot be a variable constraint in the model.

Example

Load model_tutorial_llmatlab.mph:

model = mphopen('model_tutorial_llmatlab');

comp1 = model.component('comp1');

comp1.mesh('mesh1').autoMeshSize(9);

std = model.study.create('std');

time = std.feature.create('time','Transient');

time.set('tlist','range(0,1,50)');

Edit the model to use parameter for the initial and external temperature:

model.param.set('T0','293.15[K]');

model.param.set('Text','300[K]');