The Tafel and Butler-Volmer expressions can be used to calculate the magnitude of the current due to electrolysis: this is called faradaic current. However, the electrode-electrolyte interface may also draw capacitive current due to the attraction or repulsion of ions creating an oppositely charged layer of ions to form in solution close to the electrode.
The layer of charge on the electrode and layer of opposite charge in the adjacent electrolyte is called the double layer and can be thought of as behaving like a parallel plate capacitor, since the absolute amount of charge it separates varies with the charge density on the electrode, and hence with its voltage. The physics of double layer structure and formation are highly complex and are not yet well understood. One of the simplest empirical methods to account for the observed influence of capacitance on polarization curves is to introduce a constant ideal capacitance across the electrode-electrolyte interface.
This effect can be added to via the Double Layer Capacitance condition. The capacitor stores a surface charge density
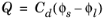
, and contributes a dynamic charging current density (
non-faradaic current) equal to
iNF = d
Q/d
t. The total current recorded in a real experiment equals: