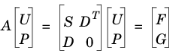The algorithm is a local smoother/preconditioner of Vanka type. It is based on the ideas in Ref. 21, Ref. 35, and Ref. 36. It is possible to describe it as a block SOR method, where the local coupling of the degrees of freedom (DOFs) determines the blocks. The important idea in this algorithm is to use Lagrange multiplier variables to form the blocks. For illustration purposes, consider the Navier-Stokes equations. For these equations the pressure variable plays the role of Lagrange multiplier. The linearized equations on discrete form have the following structure:

where U and P are the velocity and pressure degrees of freedom, respectively. The algorithm loops over the Lagrange multiplier variable DOFs (here the pressure DOFs Pj) and finds the direct connectivity to this DOF. To do so, the algorithm locates the nonzero entries in the matrix column corresponding to Pj. The row indices of the nonzero entries define the DOFs Uk, and the algorithm forms a local block matrix based on this connectivity:

One Vanka update loops over all Pj and updates

where the (.)j denotes the restriction of a vector to the rows corresponding to the block j. ω is a relaxation parameter. The algorithm does not form the inverses of the block matrices explicitly. Instead, it computes the Vanka update with a LAPACK direct solver or a GMRES iterative method subroutine call. The GMRES method is the restarted GMRES without preconditioning. The algorithm relies on the fact that it is possible to invert the submatrices Aj. If it is not possible, the algorithm gives an error message. A zero on the diagonal of A or Aj is not necessarily a problem for this updating strategy. In general, the Vanka update does not necessarily update all DOFs. This is the case for problems with weak constraints, where only a small subset of the problem’s DOFs are directly coupled to the Lagrange multipliers for the constraints. Another example is the Navier-Stokes equations coupled to other equations, but where the coupling is not directly through the pressure variable (in the k-ε turbulence model, for example). The Vanka algorithm automatically detects DOFs that are not updated by the above Vanka updating procedure and performs, for each Vanka update, a number of SSOR sweeps for these DOFs. This part of the algorithm is the SSOR update; it only works for a submatrix that has a nonzero diagonal. Just as the SOR and Jacobi preconditioner algorithms, this algorithm gives an error message if it finds zeros on the diagonal for the DOFs in the SSOR update.