The Adaptive Mesh Refinement solver algorithm and Error Estimates for the Time-Dependent Solver, The L2 Norm Error Estimate, and The Functional Error Estimate are discussed in this section.

The adaptive solver performs the following iterative algorithm (Ref. 14):

An adapted solution at t = tn is mapped to the coarse base mesh. A new adapted mesh for the time interval [tn, tn+1] is constructed by first computing a coarse solution on the base mesh in [tn, ts], where ts is the largest sample time and tn+1 = 2tn − tn−1. The error indicator is evaluated using the coarse solution at the given sample points.

In the case of an automatic time interval, a measure of the amount of refinement is computed and compared to a given requested value. If the computed value is too small or too large, the interval length is increased or decreased, respectively, which results in a new tn+1. If the interval length needs to be changed, the error indicator is sampled again using a new coarse solution. The comparison is done only once.

The new adapted mesh is obtained by using the error indicator sampled at given points in [tn, tn+1], selecting a set of elements based on the element pick function, and then finally refining these elements. The solution at tn to the PDE problem on the previous adapted mesh for [tn−1, tn] is then mapped to the new mesh for [tn, tn+1] and time integration continues until the next mesh adaptation takes place at tn+1.

Here γ is an N-vector of integers containing the number of times the element at that position should be refined, p = maxiγ(i), and N is the number of elements of the coarse base mesh.

Now, the next interval length is decreased by a given factor if ρ is larger than 120% of the requested reference value. If ρ is smaller than 80% of the reference value it is instead increased. Otherwise the interval length is kept the same.

A possible error indicator is the L2 norm of the gradient of the dependent variables (for example, sqrt(comp1.Tx^2+comp1.Ty^2) for the temperature in a 2D heat transfer model). The gradient of the dependent variable is the default value for the error indicator in most physics interfaces.

A solution on the coarse base mesh is computed in the next time interval, and the error indicator is evaluated at the points specified in the Sample points field. In this way a new adapted mesh appropriate for the next time interval can be generated. The sample points must be specified as a number between 0 and 1 because they are interpreted as being relative to the time interval under consideration. Entering a scalar value of 0.5 means that the error indicator is evaluated at the midpoint of the interval. The default value is range(0.0,0.1,1.0), which gives 11 sample points from 0 to 1.

The L2 norm error estimate relies on an assumption of a strong stability estimate for the PDE problem (satisfied, for example, for Poisson’s equation over a domain with a smooth boundary). From such an assumption, it is possible to show that there is a constant C, such that the L2 norm of the error, el, in the lth equation satisfies

where ρl is the residual in the lth equation and ql is the stability estimate derivative order. h is the local mesh element size. The adaptive solver algorithm uses the following L2-norm error indicator:

with the default value ql = 2. This formula also introduces the scaling factors sl for the residual with the default value sl = 1. The local error indicator for a mesh element is

where A is the area (volume, length) of the mesh element, and τl is the absolute value of the lth equation residual (one number per mesh element).

The functional-based estimate relies on adjoint solution error estimation. Instead of approximating the error of the solution, the adaptive solver uses the approximation of the error of a certain error functional (Ref. 17). Under rather general assumptions, it is possible to show that the error e (of a functional) can be estimated as

where el* and ρl are the error in the dual or adjoint solution to, and the residual for, the lth equation, respectively. The adaptive solver algorithm uses the following error indicator for a mesh element:

where A is the area (volume, length) of the mesh element, and τl is the absolute value of the lth equation residual (one number per mesh element). Here wl is an estimate of the adjoint solution error for the lth equation. This error is estimated in one of two ways. For both methods, the sensitivity solver finds the discrete adjoint solution. If only Lagrange element shape functions are used, the solver uses the ppr technique to compute wl as an element average of |pprint(ul*) − ul*|. Here ul* is the current computed adjoint solution for the lth equation. If not only Lagrange-element shape functions are used, then wl = hDl where Dl is an element average of . 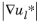The global error printed in the solver log is the sum of the error indicator for all mesh elements. See also Error Estimation — Theory and Variables.